
辛顿,杨立昆,本杰奥三位教授缘由开创深度学习Deep Learning获得2018图灵奖,巴托和萨顿两位教授缘由开创强化学习Reinforcement Learning获得2024年图灵奖。五位教授共同开立了我们现在看到的各种O1/O3及R1等推理模型基础理论,架构及算法。
强化学习介绍(前言和第一章摘录)
Reinforcement Learning An Introduction
第二版
Richard S.Sutton Andrew G.Barto
第二版前言
**自本书第一版出版以来的二十年间,人工智能领域取得了巨大的进展,其中很大一部分得益于机器学习的不断突破,包括强化学习领域的进步。**尽管令人印象深刻的计算能力的提升推动了这些进展,但理论和算法的新发展也是推动力之一。在这些进展面前,我们1998年出版的书籍迟到了第二版,最终我们在2012年开始了这个项目。我们第二版的目标与第一版一样:为读者提供清晰简明的强化学习关键思想和算法的介绍,以便所有相关领域的读者都能轻松理解。此版仍然是一个介绍性的版本,我们保持对核心、在线学习算法的关注。这一版本包括了一些在这些年间变得重要的新主题,并扩大了我们现在更好理解的主题的覆盖范围。但我们并没有试图全面覆盖这个领域,这个领域在许多不同方向上都有爆炸式增长。我们很抱歉无法包括除少数几个之外的所有贡献。
**与第一版一样,我们选择不对强化学习进行严格的正式处理,也不以最笼统的术语来表述它。**然而,自第一版以来,我们对某些主题的更深入理解需要更多的数学来解释;我们在阴影框中设置了o↵更多的数学部分,非数学倾向者可以选择跳过。 我们还使用了比第一版略有不同的符号。 在教学中,我们发现新符号有助于解决一些常见的混淆点。 它强调随机变量(用大写字母表示)和它们的实例化(用小写字母表示)之间的区别。 例如,时间步t的状态、作和奖励表示为St、At和Rt,而它们的可能值可能表示为s、a和r。 除此之外,很自然地对值函数使用小写(例如 ,v⇡)并将大写字母限制为其表格估计(例如 ,Qt(s,a)) 。 近似值函数是随机参数,因此也是小写形式(例如,(s, wt) ⇡ v⇡ (s))。向量,如作为权重向量wt(以前的✓t)和特征向量xt(以前的φt),即使它们是随机变量,也要用粗体小写字母书写。大写粗体字用于保留。
矩阵。 在第一版中,我们使用了特殊符号P0和R0,用于过渡。
概率和预期奖励。其中一个缺点是,该符号仍然没有完全刻画奖励的动态,只给出了它们的期望值,这对于动态规划是足够的,但对于强化学习来说不够。另一个缺点在这个版本中,我们使用显式符号p(s0 , r|s, a)表示下一个状态和奖励在当前状态和动作下的联合概率。所有符号上的变化都总结在第xix页的表格中。
**第二版显着扩展,其顶层组织结构已经改变。**在介绍性的第一章之后,第二版被分为三个新部分。第一部分(第2-8章)尽可能地涵盖了强化学习,而没有超出可以找到确切解决方案的表格式情况。我们涵盖了表格式情况下的学习和规划方法,以及它们在n步方法和Dyna中的统一。这部分中呈现的许多算法都是第二版的新增内容,包括UCB,Expected Sarsa,双重学习,树形备份,Q(σ),RTDP和MCTS。首先在简单的环境中彻底进行表格式情况的讨论,使核心思想能够在最简单的情境中得到发展。书的第二部分(第9-13章)然后致力于将这些思想扩展到函数逼近。它包括关于人工神经网络、傅立叶基、LSTD、基于核的方法、梯度TD和强调TD方法、平均奖励方法、真正的在线TD(λ)和策略梯度方法的新章节。第二版显著扩展了有关离策略学习的探讨,首先是在第5-7章中针对表格式情况,然后在第11和12章中进行函数逼近。另一个变化是,第二版将正向视图n步自举的概念(现在在第7章中更详细地讨论)与反向视图资格痕迹的概念(现在在第12章中独立讨论)分开。书的第三部分有关强化学习与心理学(第14章)和神经科学(第15章)的关系的大型新章节,以及包括Atari游戏、Watson的赌博策略以及AlphaGo和AlphaGo Zero的围棋程序在内的案例研究更新章节(第16章)。然而,基于必要性,我们仅包含了该领域中已完成工作的一小部分。我们的选择反映了我们长期以来对廉价的无模型方法以及其在大型应用中应具有的良好扩展性的兴趣。最后一章现在包括对强化学习未来社会影响的讨论。不管好坏,第二版的内容是第一版的两倍大。
这本书被设计为一门关于强化学习的一学期或两学期课程的主要教材。 对于一学期课程,前十章应按顺序授课,形成一个良好的核心,可以从其他章节、其他书籍(如Bertsekas和Tsitsiklis(1996)、Wiering和van Otterlo(2012)以及Szepesv´ari (2010))或文献中,根据个人口味添加其他材料。 根据学生的背景,可能需要一些关于在线监督学习的额外材料。 选项和选项模型的想法是一个自然的补充(Sutton、Precup和Singh, 1999)。 两学期课程可以覆盖所有章节以及补充材料。 本书也可作为机器学习、人工智能或神经网络等更广泛课程的一部分。 在这种情况下,可能只希望覆盖部分材料。 我们建议简要介绍第1章,接着从第2章到第2.4节,第3章开始,然后根据时间和兴趣选择剩余章节的内容。 第6章对于本课题和整本书来说至关重要。 一门着重机器学习或神经网络的课程应该涵盖第9和第10章,而一门着重人工智能或规划的课程应该涵盖第8章。 整本书中,标记了一些更难理解且对于本书其余部分不是必要的章节和部分。
带有⇤的内容可以在第一次阅读时省略,而不会在以后造成问题。一些练习题也标有⇤,表示它们更加高级,对于理解本章基础知识并不必要。
大多数章节都以一个名为“文献和历史评论”的部分结束,在这一部分中,我们将为该章节中呈现的观点来源进行归功,提供进一步阅读和进行中研究的指引,并描述相关的历史背景。尽管我们努力让这些部分具有权威性和完整性,但我们无疑地遗漏了一些重要的先前工作。对此,我们再次道歉,并欢迎纠正和补充内容,以便纳入书籍的电子版本中。
像第一版一样,这本书的新版是献给A. Harry Klopf先生的。正是Harry介绍了我们认识彼此,也是他关于大脑和人工智能的想法引领了我们长久的强化学习探索之旅。Harry接受过神经生理学训练,长期对机器智能感兴趣,他是与俄亥俄州赖特-帕特森空军基地航空电子司令部相关联的高级科学家。他对于在解释自然智能和提供机器智能基础时,过分强调寻求平衡过程,包括稳态和纠错模式分类方法的重要性感到不满。他指出,试图最大化某些内容的系统(无论是什么)在质上与寻求平衡的系统不同,而且他认为最大化系统是理解自然智能的重要方面以及构建人工智能的关键。Harry在从AFOSR获得资金支持上起到了关键作用来评估这些想法及相关想法的科学价值。这个项目在1970年代后期在马萨诸塞州立大学阿默斯特分校进行,最初由大学计算机与信息科学系的Michael Arbib、William Kilmer和Nico Spinelli教授负责,他们是大学系统神经科学控制中心的创始成员,这是一个有远见的团队,专注于神经科学与人工智能的交叉领域。Barto,一个来自密歇根大学的新博士,被聘为该项目的博士后研究员。同时,Sutton,一名斯坦福大学计算机科学和心理学专业的本科生,一直与Harry就经典条件作用中刺激时间的作用进行通信。Harry建议UMass团队让Sutton加入项目。因此,Sutton成为UMass的博士研究生,他的博士学位由已晋升为副教授的Barto指导。本书中介绍的强化学习研究正是该项目由Harry发起并受其思想启发的结果。此外,Harry也负责让我们这些作者在一起合作,这已经是一段长久而愉快的互动。通过将这本书献给Harry,我们致敬他对强化学习领域以及我们合作的重要贡献。我们还感谢Arbib教授、Kilmer教授和Spinelli教授给予我们开始探索这些想法的机会。最后,我们感谢AFOSR在我们研究的早期多年提供的慷慨支持,以及NSF在随后多年提供的慷慨支持。
我们要感谢很多人对第二版的启发和帮助。我们感谢所有在第一版中为他们的启发和帮助而致谢的人。
值得我们最深深的感激,这本版本也不会存在,如果不是他们为第一版的贡献。在那个长长的名单上,我们必须添加许多其他人,他们特别为第二版做出了贡献。多年来,我们教授这门学科的学生以各种方式做出了贡献:指出错误,提供修正意见,并且,在我们需要解释得更好的地方,表现得困惑。我们特别感谢玛莎·史汀斯特鲁普(Martha Steenstrup)在整个阅读过程中提供的详细评论。心理学和神经科学的章节,如果没有这两个领域的许多专家的帮助就无法写成。我们感谢约翰·摩尔(John Moore)多年来对动物学习实验、理论和神经科学的耐心指导,并对第14章和第15章的多个草稿进行认真阅读。我们还感谢马特·博特温尼克(Matt Botvinick)、纳撒尼尔·道(Nathaniel Daw)、彼得·达扬(Peter Dayan)和亚埃尔·尼夫(Yael Niv)对这些章节的草稿提出的深刻评论,对广泛文献的重要指导,以及在初稿中发现我们许多错误的拦截。当然,这些章节中仍然存在的错误——一定还有一些——完全是我们自己的责任。我们感谢菲尔·托马斯(Phil Thomas)帮助我们使这些章节对非心理学家和非神经科学家更易理解,并感谢彼得·斯特林(Peter Sterling)帮助我们改善表达。我们感谢吉姆·霍克(Jim Houk)介绍我们了解基底神经节中的信息处理主题,并提醒我们其他相关的神经科学方面。何塞·马丁内斯(Jos´e Mart´ınez)、特里·塞诺斯基(Terry Sejnowski)、大卫·银(David Silver)、杰瑞·泰索罗(Gerry Tesauro)、乔治奥斯·西奥库鲁斯(Georgios Theocharous)和菲尔·托马斯(Phil Thomas)慷慨地帮助我们理解他们的强化学习应用的细节,以便包含在案例研究章节中,并对这些部分的草稿提供有益意见。特别要感谢大卫·银(David Silver)在帮助我们更好地理解蒙特卡罗树搜索(Monte Carlo Tree Search)和DeepMind下围棋程序方面的帮助。我们感谢乔治·科尼达里斯(George Konidaris)在傅立叶基础部分的帮助。埃米利奥·卡托尼(Emilio Cartoni)、托马斯·塞德伯格(Thomas Cederborg)、斯特凡·德恩巴赫(Stefan Dernbach)、克莱门斯·罗森鲍姆(Clemens Rosenbaum)、帕特里克·泰勒(Patrick Taylor)、托马斯·科林(Thomas Colin)和皮埃尔-吕克·培根(Pierre-Luc Bacon)在许多重要方面为我们提供帮助,我们对此深表感激。
Sutton还要感谢艾伯塔大学强化学习与人工智能实验室的成员们对第二版的贡献。他特别感谢Rupam Mahmood在第5章中关于蒙特卡洛方法的贡献,感谢Hamid Maei对第11章中的离策略学习观点的发展,感谢Eric Graves在第13章中进行实验,感谢Shangtong Zhang复制并验证几乎所有的实验结果,感谢Kris De Asis改进第7章和第12章的新技术内容,感谢Harm van Seijen对n步方法和资格痕迹的分离提供的见解,以及(与Hado van Hasselt一起)提出的关于资格痕迹前向和后向视图的精确等价性的想法在第12章中呈现。 Sutton还要感谢艾伯塔政府和加拿大国家科学与工程研究理事会在第二版构思和撰写期间给予的支持和自由。他特别要感谢Randy Goebel在艾伯塔的研究提供了支持和远见卓识的环境。他还要感谢DeepMind在撰写本书的最后六个月中给予的支持。
最后,我们要感谢那些仔细阅读我们在互联网上发布的第二版草稿的读者。他们发现了我们忽视的许多错误,并提醒我们潜在的混淆点。
第一版前言
我们最初是在1979年末开始关注现在被称为强化学习的。当时我们都在马萨诸塞大学工作,参与其中一个最早的项目,重新探讨类似神经元的自适应元素网络可能是一种有前途的人工适应智能方法。该项目探索了A. Harry Klopf开发的“自适应系统的异稳态理论”。Harry的工作是一个丰富的思想来源,我们被允许批判性地探索这些思想,并将其与自适应系统之前的相关工作长期历史进行比较。我们的任务是将这些思想分解开来,并理解它们之间的关系及其相对重要性。这种工作至今仍在继续,但在1979年,我们开始意识到,也许最简单的一个思想,长期以来被认为理所当然,却在计算角度上受到了惊人的少关注。那就是一个学习系统想要某物,通过调整行为以最大化来自环境的特殊信号。这就是“享乐主义”学习系统的思想,或者说,正如我们现在会说的,强化学习的概念。
和其他人一样,我们感觉到强化学习在控制论和人工智能的早期已经被彻底探索过。 然而,经过仔细检查,我们发现它只被探索了一下。 虽然强化学习显然激发了一些最早的学习计算研究,但这些研究人员中的大多数已经转向其他事情,例如模式分类、监督学习和自适应控制,或者他们完全放弃了学习研究。 因此,学习如何从环境中获取某些东西所涉及的特殊问题受到的关注相对较少。回想起来,专注于这个想法是启动这一研究分支的关键步骤。在认识到这样一个基本思想尚未得到彻底探索之前,强化学习的计算研究几乎没有取得进展。
自那时起,这个领域已经走过了很长的一段路,朝多个方向不断演化和成熟。强化学习逐渐成为机器学习、人工智能和神经网络研究中最活跃的领域之一。该领域已经建立了坚实的数学基础和令人印象深刻的应用。强化学习的计算研究现在已经是一个庞大的领域,全球各地有数百名活跃的研究人员来自心理学、控制理论、人工智能和神经科学等多个学科领域。特别重要的是那些建立和发展强化学习与最优控制理论和动态规划之间关系的贡献。
互动学习以实现目标的总体问题仍然远未解决,但我们对此的理解已经显著提高。现在,我们可以将诸如时间差分学习、动态规划和函数逼近等组件性思想放置在一个整体问题的一致视角下。
我们撰写这本书的目标是提供关于强化学习的关键思想和算法的清晰简明的说明。我们希望我们的内容对所有相关学科的读者具有可读性,但我们无法详细涵盖所有这些观点。在很大程度上,我们的内容从人工智能和工程的角度出发。与其他领域的联系,我们留待他人或另一个时机来进行讨论。我们也选择不提供强化学习的严格正式处理。我们没有追求最高水平的数学抽象,并且没有依靠定理-证明的格式。我们力求选择合适的数学细节水平,引导数学倾向者朝着正确的方向前进,同时不会分散对基本思想的简单性和潜在普适性的注意力。
在某种意义上,我们已经为这本书工作了三十年,我们要感谢许多人。首先,我们要感谢那些亲自帮助我们发展本书中所呈现的整体观点的人:Harry Klopf,帮助我们认识到强化学习需要重新振兴;Chris Watkins,Dimitri Bertsekas,John Tsitsiklis和Paul Werbos,帮助我们看到与动态规划的关系的价值;John Moore和Jim Kehoe,从动物学习理论中提供的见解和启示;Oliver Selfridge,强调适应的广度和重要性;以及更一般地,我们的同事和学生在各种方式上的贡献:Ron Williams,Charles Anderson,Satinder Singh,Sridhar Mahadevan,Steve Bradtke,Bob Crites,Peter Dayan和Leemon Baird。我们对强化学习的看法通过与Paul Cohen,Paul Utgo↵,Martha Steenstrup,Gerry Tesauro,Mike Jordan,Leslie Kaelbling,Andrew Moore,Chris Atkeson,Tom Mitchell,Nils Nilsson,Stuart Russell,Tom Dietterich,Tom Dean和Bob Narendra的讨论得到了显著丰富。我们感谢Michael Littman,Gerry Tesauro,Bob Crites,Satinder Singh和Wei Zhang分别提供了第4.7节,第15.1节,第15.4节,第15.5节和第15.6节的具体内容。我们感谢空军科学研究办公室,国家科学基金会和GTE实验室长期而有远见地支持。
符号说明
Capital letters are used for random variables, whereas lower case letters are used for the values of random variables and for scalar functions. Quantities that are required to be real-valued vectors are written in bold and in lower case (even if random variables). Matrices are bold capitals.
=.相等关系是根据定义而成立的⇡ 大致相等与proportional to
Pr{X = x} probability that a random variable X takes on the value x
X ⇠ p从分布p(x)中选择的随机变量X E[X]
随机变量X的期望,即E[X] = ∑x p(x)x
argmaxa f(a) a value of a at which f(a) takes its maximal value在该值处,f(a)取得最大值。
ln x x的自然对数
ex , exp(x) the base of the natural logarithm, e ⇡ 2.71828, carried to power x ; elnx = x R set of real numbers
f:X!Y 函数f,从集合X的元素到集合Y的元素。
assignment (a, b]是a和b之间的实际区间,包括b但不包括a。
” 在“-贪婪策略”中执行随机作的概率
步长参数 γ折现率参数
λ decay-rate parameter for eligibility traces
断言 指示函数(如果谓词为真,则谓词= 1,否则为0)
In a multi-arm bandit problem:
k number of actions (arms)
离散时间步或局数。
(a)行动a的真实价值(预期奖励)q⇤(a)在时间t的估计Qt(a)。
在时间t之前动作a被选择的次数。
Ht (a) learned preference for selecting action a at time t ⇡t (a) probability of selecting action a at time t
t时刻评估给定⇡t期望奖励。
符号注解总结
在马尔可夫决策过程中:
s, s0 states
一个行动 一个奖励
S是所有非终止状态的集合。
状态集合S,包括终止状态A(s);状态s中可用的所有动作集合。
R set of all possible rewards, a finite subset of R ⇢ subset of (e.g., R ⇢ R)
2 is an element of; e.g. (s 2 S, r 2 R)
|S| number of elements in set S
离散时间步长
T, T(t) final time step of an episode, or of the episode including time step t At action at time t
St state at time t, typically due, stochastically, to St−1 and At−1
时刻t的奖励Rt,通常是由状态St−1和动作At−1随机确定。
政策(决策规则)
在确定性策略⇡下,对状态s采取的动作。
在随机策略下在状态s下采取动作a的概率为⇡。
在时间t之后返回Gt。
目光所及的地平线,前方所期待的时间步。
Gt:从t +1到t + n,或到h的n步回报(折扣和纠正)
t:h flat return (undiscounted and uncorrected) from t +1 to h (Section 5.8)
G λ-return(第12.1节)
G:h truncated, corrected λ-return (Section 12.3)
Gs, Ga λ-return, corrected by estimated state, or action, values (Section 12.8)
p (s0 , r|s, a)从状态s和动作a转移到状态s0且获得奖励r的概率p (s0 |s, a) 从状态s执行动作a转移到状态s0的概率
r(s, a)在执行动作a后来自状态s的预期即时奖励
r(s,a, s0 )在执行动作a时,从状态s转移到状态s0时的预期即时奖励
v⇡(s)在策略⇡下状态s的价值(期望回报)v⇤(s)在最优策略下状态s的价值
q(s, a)在最优策略下,状态s下采取动作a的价值。
V, Vt数组估计的状态值函数v⇡或v⇤
Q,Qt array estimates of action-value function q⇡ or q⇤
t (s) expected approximate action value; for example, t (s) =. Pa ⇡(a|s)Qt (s, a)
Ut target for estimate at time t
汇总符号说明

目录-全书591页
第二版序言
第一版序言
符号
总结
1****介绍
1.1强化学习(Reinforcement Learning)
1.2例子
1.3强化学习的要素
1.4限制和范围
1.5扩展示例: Tic-Ta Toe
1.6总结.
1.7强化学习的早期历史
2 Multi-armed Bandits 25
3 Finite Markov Decision Processes
4 Dynamic Programming
5 Monte Carlo Methods
6 Temporal-Di↵erence Learning
7 n-step Bootstrapping
8 Planning and Learning with Tabular Methods
8.1 Models and Planning
II Approximate Solution Methods
9 On-policy Prediction with Approximation
10 On-policy Control with Approximation
11 *O↵-policy Methods with Approximation
12 Eligibility Traces
13 Policy Gradient Methods 321
III Looking Deeper 339
14 Psychology
15 Neuroscience
16 Applications and Case Studies
16.1 TD-Gammon
16.2 Samuel’s Checkers Player
16.3 Watson’s Daily-Double Wagering
16.4 Optimizing Memory Control
16.5 Human-level Video Game Play
16.6 Mastering the Game of Go
16.6.1 AlphaGo
16.6.2 AlphaGo Zero
16.7 Personalized Web Services
16.8 Thermal Soaring
17 Frontiers 459
References-------- 481
Index------------- 519
1 序
**我们通过与环境互动来学习的观念可能是我们在思考学习的本质时首先想到的。当婴儿玩耍、挥动手臂或四处张望时,并没有明确的老师,但它与环境有着直接的感觉运动联系。**通过运用这种联系产生了关于因果关系、行为后果以及如何实现目标的丰富信息。在我们的一生中,这样的互动无疑是了解我们的环境和自身的主要知识来源。**无论是学开车还是进行对话,我们都在敏锐地意识到我们的环境如何对我们的行为做出反应,我们努力通过我们的行为影响发生的事情。**从互动中学习是几乎所有学习和智能理论的基本观念。
在这本书中,我们探讨了一种从交互中学习的计算方法。 我们不是直接对人或动物如何学习进行理论化,而是主要探索理想化的学习情境并评估各种学习方法的效果。 也就是说,我们采用人工智能研究人员或工程师的视角。 我们探索有助于解决科学或经济兴趣的学习问题的机器设计,通过数学分析或计算实验评估设计。 我们探索的方法称为强化学习,与其他机器学习方法相比,它更侧重于从交互中进行目标导向学习。
1.1 强化学习
**强化学习是学习如何做某事的过程,即如何将情境映射到行为,以最大化数值奖励信号。**学习者不会被告知要采取哪些行动,而是必须通过尝试来发现哪些行动获得最多的奖励。在最有趣和具有挑战性的情况下,行动可能不仅会影响即时奖励,还会影响到下一个情境,从而影响所有后续奖励。这两个特征——试错搜索和延迟奖励——是强化学习最重要的两个区别特征。
**强化学习,就像许多以“ing”结尾的名称一样,比如机器学习和登山,同时是一个问题,一类在这个问题上表现良好的解决方法,以及研究这一问题及其解决方法的领域。**使用一个名称来表示这三者都是方便的,但同时也需要保持这三者在概念上的分离。特别是在强化学习中,问题和解决方法之间的区分非常重要;不做这种区分是导致许多困惑的根源。
我们通过动力系统理论的思想,将强化学习问题形式化为部分未知马尔可夫决策过程的最优控制。这种形式化的细节需要等到第3章才能讲解,但基本思想很简单,即捕捉学习智能体与环境在时间互动中实现目标时所面临的真实问题的最重要方面。学习智能体必须能在一定程度上感知环境的状态,并且必须能够采取影响状态的行动。智能体还必须有与环境状态相关的一个或多个目标。马尔可夫决策过程旨在以简单到不能再简单的形式包括这三个方面——感知、行动和目标,而不是使它们变得琐碎。我们认为任何适合解决这类问题的方法都是强化学习方法。
**强化学习与监督学习不同,监督学习是机器学习领域中大部分研究所探讨的学习类型。**监督学习是从一个由知识外部监督者提供的带有标签示例的训练集中学习。每个示例是一个情境描述以及系统应该在该情境中采取的正确行动的标签。这种学习的目的是使系统能够推广或概括其响应,以便在训练集中不存在的情况下正确行动。这是一种重要的学习方式,但单独而言不能满足互动式学习的需求。在互动问题中,通常无法获得既正确又代表所有智能体必须行动的情景的所需行为示例。在未知领域,即人们预期学习最有益处的地方,一个智能体必须能够从自己的经验中学习。
**强化学习也不同于机器学习研究人员所谓的无监督学习,后者通常是指在未标记数据集中发现隐藏结构。**监督学习和无监督学习这两个术语似乎可以全面分类机器学习范式,但实际上并非如此。尽管人们可能会将强化学习视为一种无监督学习,因为它不依赖于正确行为示例,但强化学习试图最大化奖励信号,而不是寻找隐藏结构。在智能体人的经验中揭示结构在强化学习中确实可能有用,但单独这样做并不能解决最大化奖励信号的强化学习问题。因此,我们认为强化学习是第三个机器学习范式,与监督学习和无监督学习并列,可能还有其他范式。
**在强化学习中出现的一个挑战,而其他类型的学习中却没有的是探索和利用之间的权衡。**为了获得大量的奖励,强化学习智能体必须偏好过去尝试过并发现有效产生奖励的动作。但是为了发现这样的动作,它必须尝试之前没有选择过的动作。智能体必须利用它已经经历过的内容以获得奖励,但也必须探索以在未来做出更好的动作选择。困境在于,不能单独进行探索或利用而不在任务中失败。智能体必须尝试各种动作,并逐渐倾向于那些看起来最好的动作。在随机任务中,每个动作必须尝试多次以获得其预期奖励的可靠估计。探索与利用的困境已经被数学家们密切研究了几十年,但仍未解决。暂且我们只是指出,平衡探索和利用的整个问题在监督学习和无监督学习中甚至没有出现,至少在这些范式的最纯粹形式中没有出现。
**强化学习的另一个关键特点是,它明确地考虑了一个目标导向的智能体与不确定环境交互的整个问题。**这与许多只考虑子问题而不解决如何将其纳入更大局面的方法形成了鲜明对比。例如,我们提到许多机器学习研究人员研究了监督学习,却没有说明这种能力最终如何有用。其他的研究人员发展了具有通用目标的规划理论,但没有考虑规划在实时决策中的作用,或者规划所需的预测模型应该从何处得来的问题。尽管这些方法产生了许多有用的结果,但它们对孤立的子问题的关注是一个重要的限制。
强化学习则采取了相反的策略,从一个完整的、交互式的、目标寻求的智能体开始。 所有强化学习智能体都有明确的目标,可以感知其环境的各个方面,并可以选择作来影响其环境。此外,通常从一开始就假设智能体必须作,尽管它面临的环境存在重大不确定性。 当强化学习涉及规划时,它必须解决规划和实时行动选择之间的相互作用,以及如何获取和改进环境模型的问题。当强化学习涉及监督学习时,它这样做是出于特定原因,这些原因决定了哪些功能是关键的,哪些不是。 为了使学习研究取得进展,必须分离和研究重要的子问题,但它们应该是在完整的、互动的、寻求目标的智能体中发挥明确作用的子问题,即使完整智能体的所有细节都还不能填写。
**一个完整、互动、目标导向的智能体器并不总是意味着一个完整的有机体或机器人。**这些显然是例子,但一个完整、互动、目标导向的智能体器也可以是更大行为系统的一个组件。在这种情况下,智能体器直接与更大系统的其他部分互动,间接与更大系统的环境互动。一个简单的例子是一个监视机器人电量的智能体器,并向机器人的控制架构发送命令。这个智能体器的环境是机器人的其余部分以及机器人的环境。
第一章重点是要超越最明显的智能体和环境示例,以理解强化学习框架的普遍性。
现代强化学习最令人兴奋的一个方面是其与其他工程和科学学科之间实质性和富有成果的互动。强化学习是人工智能和机器学习长达数十年的趋势之一,向统计学、优化以及其他数学学科更加融合。例如,一些强化学习方法具有使用参数化逼近器进行学习的能力,从而解决了运筹学和控制理论中经典的“维度灾难”问题。更为独特的是,强化学习也与心理学和神经科学紧密互动,双方都获益匪浅。在所有形式的机器学习中,强化学习最接近人类和其他动物所进行的学习方式,许多强化学习的核心算法最初是受到生物学习系统启发而开发的。强化学习也做出了回馈,通过一个更好地匹配部分实证数据的动物学习的心理模型,以及大脑奖励系统部分的有影响力的模型。本书的主体部分探讨了与工程和人工智能相关的强化学习概念,并概述了与心理学和神经科学相关的内容,这些内容在第14章和第15章中有所总结。
**最后,强化学习也是人工智能回归简单一般原则的大趋势的一部分。**自1960年代后期以来,许多人工智能研究者假设没有可发现的一般原则,相反,智能是由于拥有大量特殊目的的技巧、程序和启发式方法。 有时有人说,如果我们能把足够的相关事实放进一台机器里,比如说100万或10亿,那么它就会变得智能。 基于一般原则的方法,例如搜索或学习,被描述为“弱方法”,而基于特定知识的方法被称为“强方法”。 这种观点在今天并不常见。 在我们看来,现在还为时过早:在寻找一般原则时投入的e↵ort太少,无法得出没有原则的结论。 现代人工智能现在包括许多寻找学习、搜索和决策的一般原则的研究。 目前尚不清楚钟摆会向后摆动多远,但强化学习研究无疑是向更简单、更少的人工智能一般原则摆动的一部分。
1.2 例子
理解强化学习的一个好方法是考虑一些指导其发展的示例和可能的应用场景。
• 国际象棋大师下棋。 选择既取决于计划——预测可能的回应和反回应——也取决于对特定立场和行动的可取性的直接、直观的判断。
•一个自适应控制器实时调整炼油厂操作参数。该控制器基于产量/成本/质量的权衡进行优化。
of specified marginal costs without sticking strictly to the set points originally suggested by engineers.
一只羚羊幼崽出生后几分钟就挣扎着站起来。半小时后,它以每小时20英里的速度奔跑。
•移动机器人决定是否进入新房间寻找更多垃圾收集,或开始尝试找回充电电池的站点。它的决定基于电池的当前充电水平,以及它过去有多快多轻松地找到充电站的经验。
•菲尔准备早餐。 仔细观察,即使是这种看似平凡的活动也揭示了一个复杂的条件行为和环环相扣的目标-子目标关系网络:走到橱柜前,打开它,选择一个麦片盒,然后伸手去拿、抓住和取回盒子。 需要其他复杂的、经过调整的、交互式的行为序列才能获得碗、勺子和牛奶盒。 每个步骤都涉及一系列的眼球运动,以获取信息并指导到达和运动。 人们不断快速判断如何携带这些物品,或者是否最好先将其中一些物品运送到餐桌上再获得其他物品。 每个步骤都以目标为指导,例如拿起勺子或去冰箱,并为其他目标服务,例如在麦片准备好后用勺子吃饭并最终获得营养。 无论他是否意识到,Phil都在访问有关他身体状态的信息,这些信息决定了他的营养需求、饥饿程度和食物偏好。
这些示例具有如此基本的特征,以至于容易被忽视。所有示例都涉及一个主动的决策制定者与其环境之间的互动,在这个过程中,制定者试图在对环境的不确定性下实现目标。制定者的行动允许影响环境的未来状态(例如,下一个国际象棋位置,炼油厂油罐的水平,机器人的下一个位置以及其电池的未来充电水平),从而影响制定者在以后的时间点可用的行动和机会。正确的选择需要考虑行动的间接、延迟的后果,因此可能需要远见或规划。
与此同时,在所有这些示例中,行动的影响无法完全预测;因此,智能体必须频繁监视其环境并做出适当反应。例如,菲尔必须留意他倒入碗里的牛奶,以免溢出。所有这些示例都涉及明确的目标,即智能体可以根据直接感知到的情况来判断向目标的进展。国际象棋选手知道自己是否赢了,炼油厂操作员知道正在生产多少石油,小羚羊幼崽知道什么时候摔倒,移动机器人知道电池何时耗尽,菲尔知道自己是否喜欢早餐。
在所有这些示例中,智能体都可以利用其经验随着时间的推移提高其性能。 棋手完善了他用来评估局面的直觉,从而提高了他的下法;瞪羚小牛提高了它的奔跑效率;Phil学会了简化早餐的制作。 智能体在开始时为任务带来的知识-来自以前处理相关任务的经验,或者通过设计内置到任务中,或者
进化——影响了什么对于学习有用或容易的内容,但与环境的互动对于调整行为以利用任务的特定特性是至关重要的。
1.3 强化学习的元素
除了智能体和环境之外,人们还可以确定强化学习系统的四个主要子元素:策略、奖励信号、价值函数,以及可选的环境模型。
一个策略定义了学习智能体在特定时间的行为方式。 粗略地说,策略是一个从环境感知状态到在这些状态下要采取的行动的映射。 它对应于心理学中所谓的一组刺激-反应规则或关联。 在某些情况下,策略可能是一个简单的函数或查找表,而在其他情况下,它可能涉及像搜索过程这样的广泛计算。 策略是强化学习智能体的核心,因为单独它就足以确定行为。 一般而言,策略可以是随机的,为每个行动指定概率。
奖励信号定义了强化学习问题的目标。在每个时间步上,环境向强化学习智能体发送一个称为奖励的单个数字。智能体的唯一目标是在长期内最大化总奖励。因此,奖励信号定义了对智能体来说是好事和坏事。在生物系统中,我们可以将奖励类比为快乐或痛苦的体验。它们是智能体所面临问题的即时和定义特征。奖励信号是改变策略的主要基础;如果策略选定的行动后产生较低奖励,那么策略可能会改变以在未来的情况下选择其他行动。一般来说,奖励信号可以是环境状态和采取的行动的随机函数。
奖励信号表示直接意义上的好事,而价值函数则指定从长远来看什么是好的。粗略地说,状态的价值是智能体者从该状态开始,在未来可以预期积累的奖励总额。 奖励决定了环境状态的即时、内在的可取性,而值则表示在考虑了可能遵循的状态和这些状态中可用的奖励后,状态的长期可取性。例如,一个状态可能总是产生较低的即时奖励,但仍然具有高值,因为它经常被其他产生高奖励的状态所关注。或者反之可能是真的。打个个比方,奖励有点像快乐(如果高)和痛苦(如果低),而价值对应于一种更精细、更有远见的判断,即我们对环境处于特定状态的高兴或不高兴。
奖励在某种意义上是首要的,而价值函数作为对奖励的预测则是次要的。没有奖励就不会存在价值观,估计价值的唯一目的就是为了实现更多的奖励。然而,在做出和评估决策时,我们最关心的是价值观。行动选择是基于价值判断来做出的。我们寻求能带来最高价值状态的行动,而不是最高奖励,因为这些行动从长远来看能为我们赢得最大量的奖励。不幸的是,确定价值要比确定奖励更为困难。奖励基本上是由环境直接给出的,而价值必须从环境中估计和重新估计。
1.4 限制和范围
智能体在其整个生命周期中做出的观察序列。实际上,我们考虑的几乎所有强化学习算法中最重要的组件是有效估计价值的方法。价值估计的核心作用可以说是过去六十年来关于强化学习所学到的最重要的事情。
一些强化学习系统的第四个和最后一个元素是环境的模型。这是一种模仿环境行为的东西,或者更一般地说,允许推断环境行为的方式。例如,给定一个状态和动作,模型可能会预测出接下来的状态和奖励。模型被用于规划,通过这种方式,在实际经历之前考虑可能的未来情况来决定行动的任何方式。使用模型和规划来解决强化学习问题的方法被称为基于模型的方法,与简单的无模型方法相对,后者明确地是一种试错学习者——被视为几乎是规划的相反。在第8章中,我们探索同时通过试错学习、学习环境模型以及利用模型进行规划的强化学习系统。现代强化学习涵盖了从低层次试错学习到高层次深思熟虑规划的各个方面。
强化学习在很大程度上依赖于状态的概念-作为策略和值函数的输入,以及作为模型的输入和输出。非正式地,我们可以将状态看作是向智能体传达关于某个特定时间环境情况的信号。我们在这里使用的状态的正式定义由第3章介绍的马尔可夫决策过程框架给出。然而,更一般地,我们鼓励读者遵循非正式含义,将状态视为智能体对环境可用信息的看法。实际上,我们假设状态信号是由智能体环境中名义上一部分的某种预处理系统产生的。在本书中,我们不讨论构建、更改或学习状态信号的问题(除了在第17.3节中简要提及)。我们之所以采取这种方法,并非认为状态表示不重要,而是为了全力关注决策问题。换句话说,在本书中,我们关注的不是设计状态信号,而是根据可用的状态信号决定采取什么行动。
本书中考虑的大多数强化学习方法都围绕估计价值函数展开,但解决强化学习问题并不一定需要这样做。例如,遗传算法、遗传编程、模拟退火以及其他优化方法等解决方法从不估计价值函数。这些方法应用多个静态策略,每个策略与环境的单独实例在较长的时间段内进行交互。获得最大奖励的策略以及它们的随机变体被保留到下一代策略中,并且该过程重复进行。我们将这些方法称为进化方法,因为它们的运作方式类似于生物进化产生生物体。
即使它们在各自的个体生命期间没有学习,也可以展现出高超的行为能力。 如果政策空间足够小,或者可以结构化,以便良好的政策是普遍的或易于找到,或者搜索的时间充足,那么进化方法就可以发挥作用。此外,在学习智能体无法感知其环境的完整状态的问题上,进化方法具有优势。
*我们的重点是强化学习方法,这些方法在与环境互动时进行学习,而进化方法则不会这样做*。能够利用个体行为互动的细节的方法在许多情况下比进化方法更有效率。进化方法忽略了强化学习问题的许多有用结构:它们不利用搜索的政策是一个从状态到动作的函数的事实;它们不注意个体在其一生中经过哪些状态,选择了哪些动作。在一些情况下,这样的信息可能具有误导性(例如,当状态被误解时),但更常见的情况是应该能够实现更有效的搜索。虽然进化和学习有许多共同点,并且自然地结合在一起,我们不认为单独的进化方法特别适合强化学习问题,因此我们在本书中不涵盖它们。
1.5 A一个扩展例子: Tic-Tac-Toe
为了说明强化学习的一般概念并将其与其他方法进行对比,我们接下来将更详细地考虑一个单一的示例。
考虑熟悉的井字游戏。两名玩家轮流在一个三乘三的棋盘上玩。一名玩家执X,另一名执O,直到一名玩家通过在横向、纵向或对角线上放置三个标记获胜,就像右侧显示的X玩家那样。如果棋盘填满了,没有玩家获得三连,那么游戏就是平局。因为一个熟练的玩家可以以不败之策玩游戏,所以让我们假设我们正在与一个不完美的玩家对弈,一个有时行动不正确并允许我们获胜的玩家。现在,就在这一刻。
事实上,让我们假设抽签和输棋对我们来说同样糟糕。我们如何构建一个玩家,能够发现对手玩法中的不完美之处,并学会最大化赢得比赛的机会?
虽然这是一个简单的问题,但无法通过经典技术轻松以令人满意的方式解决。 例如,博弈论中的经典“极小极大”解决方案在这里是不正确的,因为它假设对手以一种特定的玩法。例如,一个极小极大的玩家永远不会达到它可能输的游戏状态,即使事实上由于对手的不正确下棋,它总是从那个状态中赢。 顺序决策问题的经典优化方法(例如动态规划)可以计算任何对手的最优解,但需要该对手的完整规范作为输入,包括对手在每个棋盘状态下每一步的概率。 让我们假设此信息对于此问题不是先验可用的,因为它不适用于绝大多数
在实践中感兴趣。另一方面,这样的信息可以通过经验估计,在这种情况下,通过与对手进行多场比赛来进行估计。在这个问题上,我们能做到的最好的事情是首先学习对手行为的模型,达到一定的信心水平,然后应用动态规划来计算一个在给定近似对手模型的情况下的最优解。最后,这与我们在本书后面讨论的一些强化学习方法并没有太大的不同。
将这个问题应用于进化方法的一个直接结果是对可能的策略空间进行搜索,以找到一个高概率击败对手的策略。这里,策略是告诉玩家在游戏的每个状态(三乘三棋盘上X和O的每种可能配置)下应该如何移动的规则。对于每个考虑的策略,通过与对手对弈一定数量的游戏来估计其获胜概率。然后,这种评估会决定接下来考虑哪些策略。一个典型的进化方法会在策略空间中进行爬山,不断生成和评估策略,以试图获得渐进性的改进。或者,也许可以使用遗传风格的算法,维护和评估一组策略。可以应用数百种不同的优化方法。
这里是使用价值函数方法解决井字棋问题的方式。首先,我们会建立一个数字表格,每个数字对应游戏的每种可能状态。每个数字将是从该状态开始的我们获胜概率的最新估计。我们将这个估计视为状态的价值,整个表格就是经过学习的值函数。如果从状态A开始的当前获胜概率估计高于从状态B开始的,则状态A的价值高于状态B,或者被认为比状态B “更好”。假设我们总是执X,则对所有的三个X成一排的状态,获胜概率为1,因为我们已经赢了。同样地,对所有三个O成一排的状态,或是已填满的状态,正确概率为0,因为我们无法从中获胜。我们将所有其他状态的初始值设为0.5,表示我们有50%的获胜机会的猜测。
然后我们与对手进行许多比赛。 为了选择我们的移动,我们检查我们每一次可能的移动所产生的状态(棋盘上的每个空白区域一个),并在表中查找它们的当前值。 大多数时候我们贪婪地移动,选择导致价值最大的状态的棋步,即估计获胜概率最高的状态。 然而,有时我们会从其他动作中随机选择。 这些被称为探索性移动,因为它们会让我们体验到我们可能永远不会看到的状态。 在游戏中做出和考虑的棋步顺序可以如图1.1所示。
在我们玩游戏的过程中,我们改变处于游戏中的状态的数值。我们试图使它们更准确地估计获胜的概率。为了做到这一点,我们在每次贪婪移动后将状态的值“向后备份”到移动前的状态,正如图1.1中所示。更明确地说,前一个状态的当前值会更新,使其更接近后一个状态的值。这可以通过将前一个状态的值向后一个状态的值的方向移动一部分来完成。如果我们用$S_t$表示贪婪移动之前的状态,用$S_{t+1}$表示该移动之后的状态,则对$S_t$的估计值(表示为$V(S_t)$)的更新为:
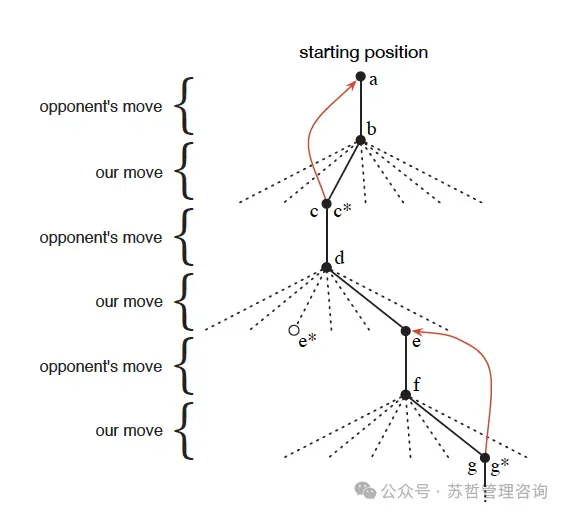
对手的走法{我们的走法{对手的走法{我们的走法{对手的走法{我们的走法{图1.1: 井字棋移动序列。 实线表示游戏中所采取的移动;虚线表示我们(我们的强化学习玩家)考虑但未采取的移动。*表示当前被估计为最佳移动。我们的第二步是一次探索性移动,这意味着即使另一个兄弟移动,即导致e⇤的移动,排名更高,我们仍然选择了这一步。探索性移动不会导致任何学习,但我们的其他每一步都会导致学习,引起如红色箭头所示的更新,其中估计值从后续节点向前继节点上移,具体详见文本。
可以写成
V (St ) V (St )+ ↵ hV (St+1) − V (St )i,
where ↵ is a small positive fraction called the step-size parameter, which influences the rate of learning. This update rule is an example of a temporal-di↵erence learning method, so called because its changes are based on adi↵erence, V (St+1)− V (St ), between estimates at two successive times.
**上面描述的方法在这项任务上表现相当好。**例如,如果随着时间适当减小步长参数,那么这种方法将收敛,对于任何固定的对手,对于每种状态,我们的玩家通过最佳策略的真实胜率。此外,采取的移动(除了探索性移动)实际上是针对这个(不完美的)对手的最佳移动。换句话说,该方法会收敛到针对这个对手下棋的最佳策略。如果随着时间的推移,步长参数并未降至零,那么该玩家也能在逐渐改变打法的对手面前表现良好。
**这个例子说明了进化方法和学习价值函数方法之间的不同之处。**为了评估一项策略,进化方法保持策略不变,并与对手进行多场比赛,或者使用对手的模型模拟多场比赛。胜利的频率提供了对使用该策略获胜的概率的无偏估计,并可用于指导下一个策略的选择。但是每次策略更改都是在进行了许多场比赛后才进行的,而且只使用每场比赛的最终结果:游戏过程中发生的事情被忽略。例如,如果玩家获胜,则将为游戏中的所有行为给予信用,而不考虑具体的关键举措。甚至给予了从未发生过的举措信用!相比之下,值函数方法允许对个别状态进行评估。最终,进化和值函数方法都搜索策略空间,但学习价值函数利用了比赛过程中可用的信息。
这个简单的例子展示了强化学习方法的一些关键特点。首先,强调在与环境(在这种情况下是对手玩家)互动时进行学习。其次,有一个明确的目标,正确的行为需要考虑到自己选择的延迟效应的规划或远见。例如,简单的强化学习玩家会学会为一个目光短浅的对手设置多步陷阱。强化学习解决方案的一个显著特点是,它可以在不使用对手模型和不对未来状态和行为序列进行明确搜索的情况下实现规划和展望的效果。
这个例子展示了强化学习的一些关键特点,但它太简单了,可能会让人觉得强化学习的局限性比实际要小。尽管井字游戏是一个双人游戏,强化学习也适用于没有外部对手的情况,也就是所谓的“与自然对抗”的情况。强化学习也不仅限于行为可以分解为独立集的问题,就像井字游戏的独立游戏那样,只有在每个集的结尾才会有奖励。当行为持续不断,并且在任何时候都可以获得不同大小的奖励时,强化学习同样适用。强化学习也适用于那些甚至不能分解为离散时间步骤的问题,就像井字游戏的下棋那样。一般原则同样适用于连续时间问题,尽管理论变得更加复杂,我们将其从本章节中省略。
**井字游戏具有相对较小的有限状态集,而强化学习可用于状态集非常大甚至无限的情况。**例如,Gerry Tesauro(1992年,1995年)将上述算法与人工神经网络结合起来,学习玩黑白棋,黑白棋有大约10^20个状态。由于状态太多,不可能全部体验。Tesauro的程序学会了比任何先前的程序都更好地玩游戏,最终甚至比世界上最好的人类玩家表现更好(见第16.1节)。人工神经网络为程序提供了从经验中泛化的能力,因此在新状态下,它根据过去面对类似状态时保存的信息选择动作,由网络确定。强化学习系统在具有如此大状态集的问题中能够工作得多好,与它从过去能够适当地泛化有密切关系。
经验。 正是在这个角色中,我们最需要强化学习中的监督学习方法。 人工神经网络和深度学习(第9.7节)并不是实现此目的的唯一方法,也不一定是最好的方法。
在这个井字棋的例子中,学习始于除了游戏规则之外没有任何先验知识,但是强化学习绝不意味着学习和智能的一张白纸观点。相反,先前的信息可以以各种方式纳入强化学习中,这对于高效学习至关重要(例如,请参见第9.5、17.4和13.1节)。在井字棋的例子中,我们还可以访问真正的状态,而当状态的部分是隐藏的,或者对学习者来说不同的状态看起来相同时,强化学习也可以被应用。
最后,井字游戏的玩家能够向前展望,并知道每个可能移动所产生的状态。为了做到这一点,它必须拥有一个游戏模型,使其能够预测其环境对可能永远不会进行的移动做出反应将如何变化。许多问题都是这样的,但在其他情况下,甚至缺乏关于行动影响的短期模型。强化学习可以应用于任何一种情况。不需要模型,但如果有模型可用或可以学习,那么模型可以很容易地使用(第8章)。
另一方面,有些强化学习方法根本不需要任何类型的环境模型。 无模型系统甚至无法考虑其环境将如何响应单个作而发生变化。 从这个意义上说,井字棋玩家相对于其对手是无模型的:它没有任何类型的对手模型。 由于模型必须具有相当的精度才能有用,因此当解决问题的真正瓶颈是难以构建足够准确的环境模型时,无模型方法可能比更复杂的方法更具优势。 无模型方法也是基于模型的方法的重要构建块。在本书中,我们用了几章来介绍无模型方法,然后讨论如何将它们用作更复杂的基于模型的方法的组成部分。
强化学习可以在系统的高层和低层都使用。尽管井字棋玩家只学到了游戏的基本走法,但没有什么阻止强化学习在更高层次上发挥作用,其中每个“动作”本身可能是应用可能复杂的问题解决方法。在分层学习系统中,强化学习可以同时在多个层次上工作。
练习1.1:自我对弈假设,与随机对手对战不同,上述强化学习算法与自身对战,双方都在学习。在这种情况下,你认为会发生什么?它会学得选择移动的不同策略吗? 练习1.2:对称性许多井字棋位置看起来不同,但实际上是相同的,因为存在对称性。我们如何修改上述描述的学习过程以利用这一点?这种改变会如何改进学习过程?现在再思考一下。假设对手没有利用对称性。在这种情况下,我们应该利用吗?对称等价位置必然具有相同的价值吗? 练习1.3:贪婪游戏假设强化学习玩家是贪婪的,即它总是选择将其带到它评价最好的位置的移动。它可能会学会比一个非贪婪玩家玩得更好还是更差?会出现什么问题?练习1.4:从探索中学习假设学习更新发生在所有移动之后,包括探索性移动。如果随着时间适当减少步长参数(但不是探索的倾向),那么状态值将收敛到不同的概率集。概念上,在我们从探索性移动中学习和不学习时分别计算的两组概率是什么?假设我们继续进行探索性移动,哪组概率更好学习?哪个会导致更多的胜利?
练习1.5:其他改进 你能想到其他改进强化学习玩家的方法吗?你能想到更好的方法来解决提出的井字棋问题吗?
1.6 总结
强化学习是一种计算方法,用于理解和自动化目标导向的学习和决策制定。它与其他计算方法不同之处在于,它强调智能体通过与环境的直接互动学习,而不需要示范监督或完整环境模型。在我们看来,强化学习是第一个严肃地解决从与环境互动学习以实现长期目标时出现的计算问题的领域。
**强化学习使用马尔可夫决策过程的形式框架来定义学习智能体和环境之间的交互,涉及状态、动作和奖励。**这个框架旨在以简单的方式表示人工智能问题的基本特征。这些特征包括因果关系感知、不确定性和非确定性感知,以及明确目标的存在。
**价值和值函数的概念对于本书中讨论的大多数强化学习方法至关重要。**我们认为值函数对于在策略空间中进行有效搜索是至关重要的。值函数的使用区分了强化学习方法和直接在策略空间中以评估整个策略为导向的进化方法。
1.7 强化学习的早期历史
强化学习的早期历史有两个主要的线索,都非常悠久而丰富,在现代强化学习中独立追寻,最终交织在一起。
第一个线索涉及通过反复尝试学习,起源于动物学习心理学。这个线索贯穿了人工智能早期的一些工作,并导致了20世纪80年代初强化学习的复兴。
**第二个线索涉及最优控制问题及其使用价值函数和动态规划解决方案。**在很大程度上,这个线索并不涉及学习。这两个线索大部分时间是独立的,但在某种程度上在一起交织。
**第三,有关时间差异方法的不太明显的线索,比如本章中使用的井字棋示例。**这三个线索在1980年代后期汇聚在一起,创造了我们在本书中介绍的现代强化学习领域。
专注于试错学习的讨论是我们在这篇简史中最熟悉的内容,也是我们有最多话要说的内容。然而,在此之前,我们简要讨论最优控制的主题。
“最优控制”这一术语在20世纪50****年代晚期开始被使用,用来描述设计控制器以在时间上最小化或最大化动态系统行为度量的问题。对此问题的一种方法是由Richard Bellman和其他人在20世纪50年代中期通过拓展哈密顿和雅可比的19世纪理论而发展的。这种方法使用动态系统状态和价值函数或“最优回报函数”的概念来定义一个被称为贝尔曼方程的泛函方程。通过解决这个方程来解决最优控制问题的方法类被称为动态规划。贝尔曼还提出了随机离散版本的最优控制问题,即马尔可夫决策过程(MDPs)。Ronald Howard在1960年为MDPs设计了策略迭代方法。所有这些都是现代强化学习理论和算法的基本要素。
动态规划被广泛认为是解决一般随机最优控制问题的唯一可行方法。 它源于贝尔曼所说的“维度的诅咒”,这意味着它的计算需求随着状态变量的数量呈指数级增长,但它仍然比任何其他通用方法更有效、适用范围更广。 自1950年代后期以来,动态规划得到了广泛的发展,包括对部分可观察的MDP的扩展(由Lovejoy调查,1991年)、许多应用程序(由White调查,1985年、1988年、1993年调查)、近似方法(由Rust调查,1996年)和异步方法(Bertsekas,1982年,1983年)。动态规划的许多优秀的现代处理方法可用(例如,Bertsekas,2005、2012;Puterman,1994;Ross,1983;Whittle,1982,1983) 。Bryson(1996) 提供了最优控制的权威历史。
最优控制和动态规划与学习之间的联系,一方面,另一方面,被辨认出来得很慢。我们不能确定是什么导致了这种分离,但它的主要原因很可能是涉及的学科和它们不同目标之间的分离。还可能导致这种分离的是动态规划被视为一种离线计算的普遍观点,这种计算基本上取决于准确的系统模型和对贝尔曼方程的解析解。此外,动态规划的最简单形式是一种按时间反向进行的计算,这使得很难看清它如何参与必须向前进行的学习过程。动态规划的一些最早的工作,比如Bellman和Dreyfus (1959)的工作,现在可能被归类为遵循学习方法。Witten (1977)的工作(下文讨论)显然符合学习和动态规划思想的结合。Werbos (1987)明确主张动态规划方法和学习方法更密切相关,并且主张动态规划与理解神经和认知机制相关。对于我们来说,动态规划方法与在线学习的完全整合并没有发生。
直到1989年Chris Watkins的工作,他使用MDP形式主义处理强化学习已被广泛采用。 从那时起,许多研究人员广泛地开发了这些关系,尤其是Dimitri Bertsekas和John Tsitsiklis(1996),他们创造了“神经动力学规划”一词来指代动态规划和人工神经网络的结合。 当前使用的另一个术语是“近似动态规划”。 这些不同的方法强调学科的不同方面,但它们都与强化学习一样,都对规避动态规划的经典缺点感兴趣。
我们认为所有关于最优控制的工作,也可以说是关于强化学习的工作。我们将强化学习方法定义为解决强化学习问题的任何有效方法,现在清楚地看到,这些问题与最优控制问题密切相关,特别是那些被表述为马尔可夫决策过程(MDP)的随机最优控制问题。因此,我们必须将最优控制的解决方法,如动态规划,也视为强化学习方法。因为几乎所有传统方法都需要完全了解被控制系统,所以说它们是强化学习的一部分,感觉有点不自然。另一方面,许多动态规划算法是增量和迭代的。像学习方法一样,它们通过逐步逼近逐渐得出正确答案。正如我们在本书的其余部分中所展示的,这些相似之处远非肤浅。关于完全和不完全知识的情况的理论和解决方法是如此密切相关,以至于我们觉得它们必须作为同一主题的一部分来考虑。
让我们现在回到另一条主要线索,导致现代强化学习领域的起源,这条线索集中在试错学习的概念上。我们只在这里简单提及主要联系点,稍后在第14.3节中更详细地讨论这个话题。根据美国心理学家R.S.伍德沃斯(1938年)的说法,试错学习的想法可以追溯到约在19世纪50年代时亚历山大·贝恩讨论的“摸索和实验学习”,更明确地,可以追溯到英国生态学家和心理学家康威·劳埃德·摩根在1894年用该术语描述他对动物行为的观察。或许第一个简洁地表达试错学习本质作为学习原则的人是爱德华·托尔达克:
对同一情况做出的几种反应中,伴随或紧随动物满足感的那些,在其他条件相同的情况下,会与情况更牢固地联系在一起,因此,当情况再次发生时,它们更有可能再次发生;而伴随或紧随动物不满的那些在其他条件相同的情况下,它们与那种情况的联系会减弱,因此,当情况再次发生时,它们更不可能发生。满足感或不满的程度越大,联系的强化或减弱也越大。
桑代克称之为“E↵ect定律”,因为它描述了强化事件对选择行动倾向的影响。 桑代克后来修改了该法律,以更好地解释有关动物学习的后续数据(例如奖励和惩罚的差异),各种形式的法律在学习理论家中引起了相当大的争议(例如,参见Gallistel,2005;Herrnstein,1970年;金波
1961年,1967年;Mazur,1994年)。尽管如此,效应定律——以一种形式或另一种形式——被广泛认为是许多行为的基本原则(例如,Hilgard和Bower,1975年;Dennett,1978年;Campbell,1960年;Cziko,1995年)。它是克拉克·赫尔(Clark Hull)的影响力学习理论(1943年,1952年)和B·F·斯金纳(B. F. Skinner)的影响力实验方法(1938年)的基础。
动物学习背景下的**“强化”一词是在索恩戴克表达效应法则之后才开始广泛应用的,在我们所知道的情况下,首次出现在1927****年英文翻译的巴甫洛夫关于条件反射的专著中。**巴甫洛夫将强化描述为由于动物接收到一个刺激(一种强化物)与另一个刺激或一个反应之间存在适当的时间关系而导致行为模式的加强。一些心理学家将强化的概念扩展到包括行为的加强和减弱,并将强化物的概念扩展到可能是刺激的省略或终止。要被视为强化物,加强或减弱必须在强化物被撤回后持续存在;仅仅吸引动物注意力或激发其行为而不产生持久变化的刺激不会被视为强化物。
在关于人工智能可能性的最早思考中,将试错学习的概念引入计算机的想法就首次出现。在**1948年的一份报告中,Alan Turing描述了一个“快乐-痛苦系统”**的设计,其工作方式符合效应法则。
当达到一个配置,其中动作是未确定的时,将对缺失数据进行随机选择,并在描述中进行临时输入,并进行应用。当出现疼痛刺激时,所有临时输入都将被取消,当出现快乐刺激时,它们都将成为永久的。(图灵,1948)
建造了许多巧妙的机电机器,展示了试错学习。 最早的可能是托马斯·罗斯 (Thomas Ross) (1933) 制造的机器,它能够在一个简单的迷宫中找到自己的路,并通过开关的设置记住路径。 1951年W.格雷·沃尔特 (Grey Walter) 构建了他的“机械”(Walter,1950年)的一个版本,能够进行简单的学习。1952年,克劳德·香农 (Claude Shannon) 展示了一只名叫忒修斯 (Theseus) 的迷宫奔跑老鼠,它通过反复试验在迷宫中找到出路,迷宫本身通过地板下的磁铁和继电器记住成功的方向(另见香农,1951年)。J.一个。Deutsch(1954) 描述了一种基于他的行为理论 (Deutsch,1953) 的迷宫解决机器,它与基于模型的强化学习 (Chapter 8) 有一些共同的特性。在他的博士论文中,Marvin Minsky(1954) 讨论了强化学习的计算模型,并描述了他构建了一个模拟机器,该机器由他称为SNARC(随机神经模拟强化计算器)的组件组成,旨在类似于大脑中可修改的突触连接(第15章)。 该网站cyberneticzoo.com包含有关这些和许多其他机电学习机的大量信息。
建造电机学习机器为编程数字计算机执行各种类型的学习铺平了道路,其中一些实施了试错学习。Farley和Clark(1954年)描述了神经网络的数字模拟。
**通过试错学习的机器很快将注意力转移到了泛化和模式识别,即从强化学习转向监督学习(Clark和Farley,1955)。**这引起一种对这些学习类型关系的混淆态势。许多研究人员认为他们在研究强化学习,实际上他们在研究监督学习。例如,人工神经网络先驱Rosenblatt(1962)和Widrow以及Ho(1960)明显受到强化学习的启发——他们使用奖励和惩罚的术语,但他们研究的系统是适合模式识别和感知学习的监督学习系统。即使在今天,一些研究人员和教科书也会将这些学习类型的区别最小化或模糊。例如,一些教科书使用术语“试错”来描述从训练实例中学习的人工神经网络。这是可以理解的混淆,因为这些网络使用错误信息来更新连接权重,但这忽略了试错学习的基本特征,即基于评估反馈选择动作,而不依赖于正确动作的知识。
**部分由于这些混淆,对真正的试错学习的研究在1960年代和1970年代变得很少见,尽管有明显的例外。**在1960年代,术语“强化”和“强化学习”首次在工程文献中用于描述试错学习的工程用途(例如,Waltz和Fu,1965年;Mendel,1966年;Fu,1970;Mendel和McClaren,1970年)。Minsky的论文《迈向人工智能的步骤》(Steps Towards Artificial Intelligence,Minsky,1961年)特别有影响力,该论文讨论了与试错学习相关的几个问题,包括预测、期望以及他所说的复杂强化学习系统的基本学分分配问题:你如何在可能涉及产生成功的许多决策中分配成功的学分? 从某种意义上说,我们在本书中讨论的所有方法都是为了解决这个问题。 明斯基的论文今天非常值得一读。
在接下来的几段中,我们将讨论20世纪60年代和70年代对真正的试错学习的计算和理论研究相对忽视的其他例外情况和部分例外情况。
新西兰研究者约翰·安德里发展了一个名为STeLLA的系统,通过与环境的互动进行试错学习。该系统包括世界的内部模型,后来又增加了一个“内部独白”来处理隐藏状态的问题(Andreae, 1963, 1969; Andreae and Cashin, 1969)。安德里后来的工作(1977年)更加强调从教师那里学习,但仍包括试错学习,生成新事件是系统的目标之一。该工作的一个特点是在Andreae (1998)中更全面阐述的“泄露回传过程”,实现了类似于我们描述的反向更新操作的信用分配机制。不幸的是,他的开创性研究并不为人知,并没有对随后的强化学习研究产生很大影响。最近有相关综述可供参考(Andreae, 2017a,b)。
更有影响力的是Donald Michie的工作。在1961年和1963年,他描述了一个简单的试错学习系统,用于学习如何下井字棋(或零和字(naughts)。
**棋盘游戏(井字棋)学习引擎(Matchbox Educable Naughts and Crosses Engine)被称为MENACE。**它由每种可能的游戏局面的一个火柴盒组成,每个火柴盒内含有一定数量的彩色珠子,每一种颜色对应当前局面下的可能移动。通过从对应当前游戏局面的火柴盒中随机取出一颗珠子,可以确定MENACE的移动动作。游戏结束时,会根据MENACE的决策情况在使用的火柴盒中添加或移除珠子以奖励或惩罚。Michie和Chambers(1968)描述了另一个井字棋强化学习引擎称为GLEE(Game Learning Expectimaxing Engine)和一个强化学习控制器称为BOXES。他们将BOXES应用于学习基于仅在杆倒下或小车到达轨道末端时发生错误信号的平衡杆的任务。这个任务是根据Widrow和Smith(1964)早期工作进行调整的,他们使用监督学习方法,假定已经能够平衡杆的老师的指导。Michie和Chambers的平衡杆版本是在不完全了解条件下的强化学习任务的最佳早期示例之一。它影响了后来许多强化学习方面的工作,始于我们自己的一些研究(Barto,Sutton和Anderson,1983;Sutton,1984)。Michie(1974)一贯强调试错和学习作为人工智能的基本要素。
Widrow, Gupta和Maitra(1973年)修改了Widrow和Ho(1960年)的最小均方(LMS)算法,以产生一种可以从成功和失败信号中学习的强化学习规则,而不是从训练样本中学习。他们称这种学习形式为“有选择性的自举适应”,并将其描述为“与评论家一起学习”而不是“与老师一起学习”。他们分析了这个规则,并展示了它如何学会玩21点。这是Widrow在强化学习领域的孤立冒险,他在监督学习方面的贡献更具影响力。我们对“评论家”一词的使用源自Widrow,Gupta和Maitra的论文。Buchanan,Mitchell,Smith和Johnson(1978年)在机器学习的上下文中独立使用了评论家这个术语(参见Dietterich和Buchanan,1984年),但对于他们来说,评论家是能够做更多事情而不仅仅是评估表现的专家系统。
学习自动机的研究对导致现代强化学习研究的试错线程产生了更直接的影响。这些方法用于解决一个非关联性、纯选择性学习问题,被称为k臂老虎机,类比于一个老虎机,有k个手柄。学习自动机是简单、低内存的机器,用于提高这些问题中奖励的概率。学习自动机起源于俄罗斯数学家和物理学家M.L. Tsetlin及其同事在1960年代开展的工作(1973年由Tsetlin在世后发表),自那时起在工程领域得到了广泛发展(请参阅Narendra和Thathachar,1974年,1989年)。这些发展包括对随机学习自动机的研究,这些方法是根据奖励信号更新行动概率的方法。尽管不是根据随机学习自动机的传统发展起来的,Harth和Tzanakou的(1974年) Alopex算法(用于模式提取算法)是一种用于检测行动与奖励之间相关性的随机方法,影响了我们早期研究的一些内容(Barto,Sutton和Brouwer,1981年)。随机学习自动机可以追溯到早期在心理学领域的研究,始于William Estes(1950年)对学习的统计理论的努力,后来由其他人进一步发展(Bush和Mosteller,1955年;Sternberg,1963年)。
心理学中发展起来的统计学习理论被经济学研究者采纳,导致了经济学领域的一系列研究,专门致力于强化学习。这项工作始于1973年,当时将Bush和Mosteller的学习理论应用于一系列经典经济模型(Cross,1973)。这项研究的一个目标是研究更像真实人类而不是传统理想化经济人的人工智能体(Arthur,1991)。这种方法扩展到了在博弈论背景下对强化学习的研究。经济学中的强化学习在很大程度上是独立于人工智能早期的强化学习工作发展而来的,尽管游戏理论仍是两个领域感兴趣的主题(超出本书范围)。Camerer(2011)讨论了经济学中的强化学习传统,Now´e,Vrancx和De Hauwere(2012)从多智能体扩展的角度提供了该主题的概述,这也是我们在本书中介绍的方法。在博弈论背景下的强化学习是一门与用于玩井字游戏、跳棋和其他娱乐游戏的强化学习截然不同的学科。例如,Szita(2012)提供了强化学习和游戏这方面的概述。
约翰·荷兰(1975年)概述了基于选择性原则的自适应系统的一般理论。他早期的研究主要涉及试错,主要以非联想形式出现,如进化方法和k臂老虎机。在1976年和1986年更全面地介绍了分类器系统,真正的强化学习系统包括联想和值函数。荷兰分类器系统的一个关键组成部分是用于信用分配的“火灾队算法”,这与我们在井字游戏示例中使用的时间差异算法密切相关,并在第6章中讨论。另一个关键组成部分是遗传算法,一种进化方法,其作用是进化出有用的表示。分类器系统已经被许多研究人员广泛发展,形成了强化学习研究的一个重要分支(由Urbanowicz和Moore,2009年评论),但遗传算法——我们不认为单独作为强化学习系统——受到了更多关注,以及其他用于进化计算的方法(例如,Fogel,Owens和Walsh,1966年;Koza,1992年)。
对恢复人工智能中强化学习的试错线负有责任的人是Harry Klopf(1972,1975,1982) 。Klopf认识到,随着学习研究人员几乎完全专注于监督学习,适应性行为的基本方面正在丢失。 根据克洛普夫的说法,缺少的是行为的享乐方面:从环境中实现某种结果的驱动力,控制环境朝着预期目的和远离不希望的目的(参见第15.9节)。 这是试错学习的基本思想。 克洛普夫的思想对作者的影响特别大,因为我们对它们的评估(Barto和Sutton,1981a)使我们认识到监督学习和强化学习之间的区别,并最终关注强化学习。 我们和同事们完成的大部分早期工作都是为了证明强化学习和监督学习确实是不同的(Barto,Sutton,and Brouwer,1981; Barto和Sutton,1981b; Barto和Anandan,1985年)。 其他研究表明强化学习如何解决人工神经中的重要问题网络学习,特别是如何产生多层网络的学习算法(Barto,Anderson和Sutton,1982年;Barto和Anderson,1985年;Barto,1985年,1986年;Barto和Jordan,1987年;见第15.10节)。
**我们现在转向强化学习历史的第三个主线,即与时间差分学习相关的内容。**时间差分学习方法在于通过时间上连续的同一量的估计之间的差异来驱动。例如,在井字棋的例子中,这种方法是独特的,因为它衡量了获胜的概率的变化。这个主线相对较小且不太明显,但在这个领域中扮演了一个特别重要的角色,部分原因在于时间差分方法似乎是强化学习中的一种新颖独特方法。
时间差异学习的起源部分源于动物学习心理学,特别是二次强化剂的概念。二次强化剂是一个刺激,已经与食物或疼痛等主要强化剂配对,结果具有类似的强化特性。明斯基(1954年)可能是第一个意识到这一心理原则对人工学习系统可能很重要的人。阿瑟·塞缪尔(1959年)是第一个提出并实施包含时间差异观念的学习方法的人,作为他著名的跳棋程序的一部分(第16.2节)。
Samuel没有提到Minsky的工作,也没有提到与动物学习的可能联系。他的灵感显然来自于克劳德·香农(1950)的建议,即计算机可以被编程以使用评估函数来下棋,并且通过在线修改这一功能可以改善其游戏水平。(可能这些香农的想法也影响了贝尔曼,但我们不知道有任何证据表明这一点。)Minsky在他的《步骤》一文中(1961年)广泛讨论了Samuel的工作,提出了与自然和人工次级强化理论的连接。
**我们已经讨论过,在跟随Minsky和Samuel的工作之后的十年中,对试错学习几乎没有进行过多的计算工作,似乎对时序差分学习根本没有进行过任何计算工作。**1972年,Klopfb将试错学习与时序差分学习的一个重要组成部分结合在一起。Klopf对能够扩展到大型系统中学习的原则感兴趣,因此对局部强化的概念产生兴趣,即整体学习系统的子组件可以相互强化。他发展了“泛强化”的概念,即每个组件(名义上,每个神经元)都将其所有输入视为强化的术语:兴奋性输入作为奖励,抑制性输入作为惩罚。这与我们现在所知的时序差分学习不是同一个概念,回顾起来,它距离Samuel的工作更远。另一方面,Klopf将这个想法与试错学习联系起来,并将其与动物学习心理学的大量经验数据库联系起来。
Sutton (1978a,b,c)进一步发展了Klopf的想法,特别是与动物学习理论的联系,描述了由时间上连续的预测变化驱动的学习规则。他和Barto进一步完善了这些想法,并基于时间差分学习发展了经典条件作用的心理模型(Sutton and Barto, 1981a; Barto and Sutton, 1982)。随后出现了几种基于时间差分学习的经典条件作用的其他有影响力的心理模型(例如,Klopf, 1988; Moore et al.)。
**1986年:Sutton和Barto(1987,1990年)。**在此时开发的一些神经科学模型在时序差分学习方面得到了很好的解释(Hawkins和Kandel,1984年;Byrne、Gingrich和Baxter,1990年;Gelperin、Hopfield和Tank,1985年;Tesauro,1986年;Friston等,1994年),尽管在大多数情况下并不存在历史联系。
**我们早期的强化学习工作受到动物学习理论和Klopf工作的强烈影响。**与Minsky的“Steps”论文和Samuel的跳棋玩家的关系只有在之后才得到承认。 然而,到1981年,我们完全意识到上面提到的所有先前工作都是时间分和试错线索的一部分。 此时,我们开发了一种将时间差异学习与试错学习相结合的方法,称为演员-评论家架构,并将该方法应用于Michie和Chambers的极平衡问题(Barto、Sutton和Anderson,1983)。 这种方法在Sutton(1984) 的博士论文中得到了广泛的研究,并在Anderson(1986) 的博士论文中扩展到使用反向传播神经网络。 大约在这个时候,Holland(1986) 以他的bucket-brigade算法的形式将时间差异思想显式地整合到他的分类器系统中。Sutton(1988) 迈出了关键的一步,将时间分离学习与控制分离,将其视为一种通用的预测方法。 该论文还介绍了TD(λ) 算法并证明了它的一些收敛特性。
**在我们1981年对演员-评论架构的工作进行最后整理时,我们发现了Ian Witten (1977, 1976a)的一篇论文,该论文似乎是最早关于时间差分学习规则的出版物。**他提出了我们现在称之为表格TD(0)的方法,用作解决马尔科夫决策过程的自适应控制器的一部分。这项工作最初于1974年提交进行期刊出版,同时也出现在Witten的1976年博士论文中。Witten的工作是Andreae早期对STeLLA和其他试错学习系统进行实验的后代。因此,Witten的1977年论文涵盖了强化学习研究的两大主要分支-试错学习和最优控制-同时对时间差分学习做出了独特的早期贡献。
1989年,随着Chris Watkins对Q-learning的发展,时间差异和最优控制线程被完全结合在一起。 这项工作扩展并整合了强化学习研究的所有三个线索中的先前工作。Paul Werbos(1987) 自1977年以来通过主张试错学习和动态规划的融合,为这种整合做出了贡献。 到Watkins工作时,强化学习研究已经有了巨大的增长,主要是在人工智能的机器学习子领域,但也在更广泛的人工神经网络和人工智能方面。1992年,Gerry Tesauro的西洋双陆棋游戏程序TD-Gammon取得了巨大成功,为该领域带来了额外的关注。
自第一版该书出版以来,神经科学的一个繁荣子领域发展起来,专注于强化学习算法与神经系统中的强化学习之间的关系。其中最值得注意的是时间差分算法的行为与大脑中多巴胺产生神经元的活动之间的惊人相似性,一些研究者指出了这一点(Friston等,1994年;Barto,1995年;Houk,Adams和Barto,1995年;Montague,Dayan和Sejnowski,1996年;Schultz,Dayan和Montague,1997年)。第15章介绍了这一令人兴奋的强化学习领域。
近年来在强化学习领域所作出的贡献数不胜数,在这篇简要的叙述中无法一一列举;我们在各自章节末尾引用了其中许多。
文献注释
有关强化学习的其他一般性介绍,我们建议读者参考Szepesv’ari(2010)、Bertsekas和Tsitsiklis(1996)、Kaelbling(1993a) 以及Sugiyama、Hachiya和Morimura(2013) 的书籍。 采取控制或运筹学视角的书籍包括Si、Barto、Powell和Wunsch(2004)、Powell(2011)、Lewis和Liu(2012) 以及Bertsekas(2012) 的书籍。Cao(2009) 的评论将强化学习置于随机动态系统学习和优化的其他方法的背景下。 《机器学习》杂志的三期特刊侧重于强化学习:Sutton(1992a)、Kaelbling(1996) 和Singh(2002)。 有用的调查由Barto(1995b) 提供;Kaelbling、Littman和Moore(1996);以及Keerthi和Ravindran(1997) 。 Weiring和van Otterlo(2012) 编辑的这本书对最近的发展进行了很好的概述。
表格解决方法
在本书的这一部分中,我们以最简单的形式描述了强化学习算法的几乎所有核心思想:状态和动作空间足够小,可以将近似值函数表示为数组或表。在这种情况下,这些方法通常可以找到精确的解,也就是说,它们通常可以准确找到最优值函数和最优策略。这与本书的后续部分描述的近似方法形成对比,后者只能找到近似解,但换来的是可以有效应用于更大问题的优势。
这部分书籍的第一章描述了针对特殊情况的强化学习问题的解决方法,即只有一个状态的情况,称为赌博机问题。第二章描述了我们在本书的其余部分中处理的一般问题形式——有限马尔可夫决策过程及其主要概念,包括贝尔曼方程和值函数。
接下来的三章描述了解决有限马尔可夫决策问题的三类基本方法:动态规划、蒙特卡洛方法和时间差异学习。 每类方法都有其优点和缺点。 动态规划方法在数学上已经发展得很好,但需要一个完整而准确的环境模型。Monte Carlo方法不需要模型,在概念上很简单,但不太适合逐步增量计算。最后,temporal-di↵erence方法不需要模型,并且是完全增量的,但分析起来更复杂。 这些方法在效率和收敛速度方面也存在多种差异。
这两章描述了如何将这三类方法结合起来,以获得它们各自的优点。其中一章描述了如何通过多步自举方法将蒙特卡罗方法的优势与时序差分方法的优势结合起来。在本书的这一部分的最后一章中,我们展示了如何将时序差分学习方法与模型学习和规划方法(例如动态规划)结合起来,以完整而统一地解决表格强化学习问题。
第二章****多臂老虎机
强化学习与其他类型的学习区别于其他类型的学习的最重要特征是它使用训练信息来评估所采取的行动,而不是通过给出正确的行动来指导。 这就是需要积极探索的原因,需要明确地寻找良好的行为。 纯粹的评估性反馈表示所采取的行动有多好,但不是它可能的最佳还是最差的行动。 另一方面,纯粹的指导性反馈表明要采取的正确行动,与实际采取的行动无关。 这种反馈是监督学习的基础,它包括大部分模式分类、人工神经网络和系统识别。 在纯粹的形式中,这两种类型的反馈非常不同:评价性反馈完全取决于所采取的行动,而指导性反馈则独立于所采取的行动。
在本章中,我们在一个简化的环境中研究强化学习的评价方面,一个不涉及学习在多个情况下行动的方面。 这种非关联设置是大多数涉及评估反馈的先前工作已经完成的设置,它避免了完全强化学习问题的大部分复杂性。 研究这个案例使我们能够最清楚地看到评价性反馈如何与指导性反馈区分开来,但又可以与指导性反馈相结合。
我们探讨的特定非关联评价反馈问题是k武装老虎机问题的简单版本。 我们用这个问题来介绍一些基本的学习方法,我们将在后面的章节中扩展这些方法,以应用于完全强化学习问题。 在本章的结尾,我们通过讨论当老虎机问题变得关联时会发生什么,即当最佳行动取决于情况时,我们向完全强化学习问题更近了一步。
2.1 一个k臂赌博机问题
**考虑以下学习问题。 您反复面临k个不同的选项或作之间的选择。**每次选择后,您都会收到一个数字奖励,该奖励是从稳态概率分布中选择的,具体取决于您选择的作。 你
目标是在一定时间段内最大化预期总奖励,例如,在1000个动作选择或时间步骤内。
这是k臂老虎机问题的原始形式,以一臂老虎机作为类比命名,不同之处在于它有k个杠杆而不是一个。每次动作选择就像是拉动老虎机的一个杠杆,奖励是命中大奖的支付。通过重复的动作选择,您要集中行动在最好的杠杆上,最大化您的赢利。另一个类比是医生在一系列重病患者中选择实验性治疗方法。每个动作是选择一种治疗方法,每个奖励是患者的生存或健康。今天,“老虎机问题”这个术语有时用于描述上述问题的泛化,但在本书中,我们仅用它来指代这个简单情况。
在我们的k武装老虎机问题中,如果选择了该作,则每个k个作都有一个预期或平均奖励;我们将其称为该作的值。 我们将时间步t上选择的动作表示为At,将相应的奖励表示为Rt。 任意作a的值,表示为q⇤(a),是给定选择a的预期奖励:
q*(a) = E[Rt | At = a] .
如果你知道每个动作的价值,那么解决K臂老虎机问题就会显得很琐碎:你将始终选择价值最高的动作。我们假设您并不确定动作的价值,尽管您可能有估计值。我们将在时间步骤t中将动作a的估计值表示为Qt(a)。我们希望Qt(a)接近q⇤(a)。
如果您保持对行动价值的估计,那么在任何时间步骤中至少有一个行动的估计值最大。我们将这些称为贪婪行动。当您选择这些行动之一时,我们说您正在利用当前对行动价值的了解。如果您选择的是非贪婪行动之一,那么我们说您正在探索,因为这能够改善您对非贪婪行动价值的估计。利用是在最大化一步预期奖励时应采取的正确行动,但长期来看,探索可能会产生更大的总体奖励。例如,假设某个贪婪行动的价值是确定的,而其他几个行动被估计为几乎一样好,但存在较大的不确定性。不确定性如此之大,以至于这些其他行动中至少有一个很可能比贪婪行动实际更好,但您不知道哪一个。如果您有很多时间步来选择行动,那么探索非贪婪行动并发现哪些优于贪婪行动可能更好。在探索期间,奖励较低,但从长远来看,奖励更高,因为在发现更好的行动之后,您可以多次利用它们。由于不可能在任何单个行动选择中同时进行探索和利用,人们经常提到探索与利用之间的”冲突”。
在任何特定情况下,探索还是利用更好都取决于估计值的精确值、不确定性和剩余步骤的数量。 对于武装强盗和相关问题的特定数学公式,有许多复杂的方法可以平衡探索和开发。
然而,大多数这些方法对数据的平稳性和先验知识做出了强烈的假设,这些假设在大多数应用和我们在后续章节中考虑的完整强化学习问题中要么被违反,要么不可能验证。当这些方法的理论假设不适用时,它们的最优性或有界损失的保证并不能给人带来太多安慰。
在这本书中,我们不用担心如何以复杂的方式平衡探索和利用;我们只需要担心如何平衡它们。在本章中,我们提出了几种简单的平衡方法来解决k臂老虎机问题,并展示它们比总是利用的方法要好得多。平衡探索和利用的需要是强化学习中的一个独特挑战;我们这个版本的k臂老虎机问题的简单性使我们能够以特别清晰的形式展示这一点。
2.2****行动值方法
我们首先着眼于估计动作值的方法,以及利用这些估计值做出动作选择决策的方法,这两者我们合称为“动作值估计方法”。
选定动作的一种自然方式来估计这一点是通过对实际收到的奖励进行平均:
![]() (2.1)
(2.1)
当分母为零时,我们将Qt(a)定义为一些默认值,比如0。当分母趋向于无穷大时,根据大数定律,Qt(a)收敛到
q*(a).我们称之为样本平均方法来估计动作值,因为每个
估计是相关奖励样本的平均值。当然,这只是估计行动值的一种方法,并不一定是最好的方法。尽管如此,现在让我们继续使用这种简单的估计方法,并转向估计如何用来选择行动。
最简单的动作选择规则是选择估计值最高的动作之一,也就是在前一节中定义的贪婪动作之一。如果存在多个贪婪动作,则可以以某种任意的方式在它们之间进行选择,也许是随机地。我们将这种贪婪动作选择方法写为:
![]() (2.2)
(2.2)
argmax表示使得接下来的表达式最大化的动作a(如有并列则随机选择)。贪婪行为选择总是利用当前知识来最大化即时奖励;它不会花任何时间去采样表面上较差的动作以查看它们是否实际上更好。一种简单的替代方法是大部分时间行为贪婪,但偶尔,例如以较小概率ε,选择随机方式。
从所有具有相同概率的动作中独立选择,而不考虑动作-值估计。我们将使用这种近似贪心动作选择规则的方法称为“ε-greedy方法”。这些方法的一个优势是,随着步数增加至无穷,每个动作将被采样无限次,从而确保所有的Qt (a)都收敛到各自的q⇤(a)。当然,这意味着选择最佳动作的概率收敛至大于1-ε,即接近确定性。然而,这仅是渐近保证,并对方法的实际有效性没有太多说明。
在“ε-greedy”动作选择中,对于两个动作和ε = 0.5的情况,选择贪婪动作的概率是多少?
2.3 十臂测试平台
为了粗略评估贪婪和ε-贪婪行动值方法的相对有效性,我们在一组测试问题上对它们进行了数值比较。这是一组由k = 10随机生成的2000个臂老虎机问题。对于每个老虎机问题,如图2.1所示,行动值q⇤(a),a = 1, … , 10,。
以下省略,请参考作者原著。
文章来源: 微信公众号,原始发表时间:2025年03月07日。