在机器学习的世界里,有一个函数几乎无处不在:Softmax
Softmax将神经网络最后一层的打分变成一组概率,让模型能用“我有多确定”来回答问题。乍看,这只是一个便利的数学小工具;然而当我们把目光移向 19 世纪的统计力学,再回到 20 世纪的信息论,再落脚于今天的深度学习,会发现 Softmax 是一座跨越三个时代的桥梁——其桥墩正是“熵”这一概念。
一、Softmax 是如何工作的?
设想我们要让模型判断图像中是否有猫。模型在“有猫”“没猫”两个选项上各给出一个分数,这些分数可能是任何实数。Softmax 把它们转换为概率

这个公式背后的思想非常简单而深刻:它利用指数函数将任意实数映射为正数,并通过归一化确保所有概率之和为 1。由于指数函数是单调递增的,打分高的类别将获得更大的概率,这与人类的直觉——“高分代表更有可能”——完全一致。
温度参数 T是 Softmax 中一个极具物理意味的部分。它控制输出分布的“尖锐程度”:当 T 很小时(趋近于 0),Softmax 几乎将所有概率压缩到分数最高的类别上,表现出一种“贪婪”的决策风格;而当 T 很大时,分数差异被淡化,概率分布变得更加平坦,模型变得“保守”或“探索性更强”。
二、玻尔兹曼分布:Softmax 的物理原型
Softmax 的形式与物理中的玻尔兹曼分布几乎一模一样。玻尔兹曼分布描述的是:在某一温度下,热平衡系统中粒子出现在不同能级上的概率。

能量越低的状态,所对应的概率越高。这正符合我们对自然系统的基本认知:系统倾向于向低能态演化。在这里,kk 是玻尔兹曼常数,用于将能量与温度联系起来。
如果我们将 Softmax 中的打分看作“负能量”,就可以看到它与玻尔兹曼分布在结构上的对应关系。机器学习中的“高分优先”变成了物理世界中的“低能偏好”,一正一负,逻辑一致。
三、熵:统计力学与信息论的共同灵魂
熵是连接 Softmax 与玻尔兹曼的核心概念。它同时存在于两门学科之中,形式几乎相同:
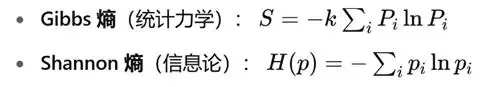
在统计物理中,熵衡量系统微观状态的“混乱度”或“无序程度”;在信息论中,熵衡量一组概率分布的不确定性,也就是在进行最优编码时的“最低码长期望”。
1957 年,E.T. Jaynes 提出了“最大熵原理”:在只有部分信息(比如平均能量)约束的情况下,我们应当选取熵最大的概率分布,因为它在不引入额外假设的前提下最大限度地保留了不确定性。这种观点把统计物理从一个经验性的学科转化为信息推理的分支。
四、Softmax 与最大熵的隐秘联系
1、为什么“最大熵”也会把我们带到 Softmax?
Softmax并不仅是一个数学变换,它其实就是最大熵原理在“已知期望打分”这一约束下的最优解。换句话说,如果我们知道模型打出的分数,并要求最终概率分布 满足
-
概率归一化:

-
给定平均打分:
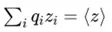
那么,在所有满足这两个条件的概率分布中,Softmax是熵最大的那一个。
数学上,我们通过极值化下列函数求解:
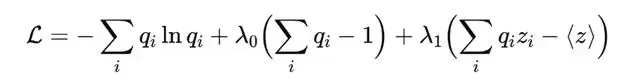
对 求导数并令其为零,我们就会发现:
![]()
这正是 Softmax 的形式。如果我们将,就可以解释 T 为一种温度参数,用来调控分布的“锐利程度”。
2、Softmax 是指数族分布的典范成员
统计学中有一个重要概念叫做“指数族分布”(Exponential Family)。所有满足一定约束条件、最大化熵的分布都会属于这个族。Softmax 恰好是当你知道分数期望(或对数似然)时,推导出来的最简指数族模型之一。
这意味着,Softmax 并不是偶然选出来的;它是一个“在最小前提下符合推断原则”的自然选择。
3、交叉熵训练 = 最小化“多余熵” = 逼近热平衡
在神经网络训练过程中,我们常用的目标函数是交叉熵:
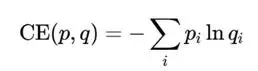
它可以被拆解为两部分:
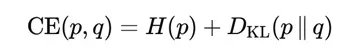
其中第一项是数据分布本身的熵,不依赖于模型参数;第二项是Kullback–Leibler 散度,衡量模型分布 q 偏离真实分布 p 的程度。
KL散度在统计力学中对应的是系统的“多余自由能”,即系统当前状态与平衡态之间的“距离”。因此,训练神经网络、最小化交叉熵,其实就是一个将系统逐步推进到热平衡的过程。
4、最大熵与最小自由能的双面性
在热力学中,系统自发演化的方向是自由能最小。在信息论中,系统推断的目标是熵最大。表面上看,这两者相互矛盾,实则互为镜像:
- 保持平均能量恒定时,最大熵状态对应最小自由能。
- 保持分类标签或输出约束时,最小交叉熵对应最大推断熵。
这种“对偶关系”说明:Softmax 不仅是一个数据驱动的模型输出层,它还内嵌了关于如何在不确定性中做出最合理决策的深刻哲学。
五、温度、探索与模拟退火
Softmax 的温度参数并不是纯粹的数学技巧,它源自物理中的“模拟退火”过程。模拟退火是一种优化算法,通过模拟粒子在高温下的随机运动,帮助系统逃出局部最优,然后逐步降温,使其最终落入全局最优解附近。
同样,在机器学习中,高温 Softmax 会鼓励模型更广泛地探索可能性,而低温 Softmax 会令模型更加坚定地做出选择。在强化学习、序列生成、策略搜索等任务中,温度控制成为了一种重要的策略参数。
六、结语:从粒子到比特,从能量到概率
Softmax 的普及并非偶然,它是一种让模型“在已知约束下输出信息最少、却又最合理猜测”的机制。它借来了玻尔兹曼分布的外衣,也继承了最大熵原理的灵魂。在信息缺乏时,它选择最大化混乱;在数据约束到来时,它又能迅速收敛。于是,一段跨越百年的学术脉络终在这一行指数函数中汇流——
统计力学告诉我们:熵决定物质运动;信息论告诉我们:熵决定知识更新;深度学习告诉我们:熵还能驱动智能。
在模型最后一次将分数变成概率的那一刻,Softmax 让“比特”与“粒子”说同一种语言。