词向量模型可能有的疑惑:词向量的维度大概多少才够? $$ n > 8.33logN $$ 其中N是词表的大小,n 就是词向量维度
词向量是基于 Skip Gram 模型的,所以我们要计算的不是词平均熵,而是整个 Skip Gram 模型的平均熵,假设词对(wi,wj) 的频率是p(wi,wj),那么可以估算它的熵为:
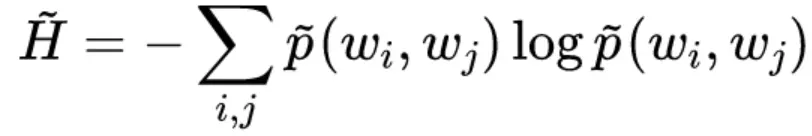
不同的词向量训练目标也有所差异,有些是在拟合联合概率p(wj,wi) ,有些是在拟合条件概率p(wj|wi),统一假设词向量模型为:
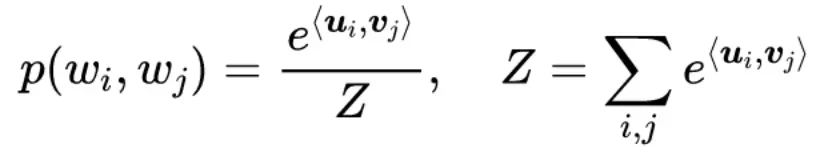
其中u,v代表两套不同的词向量(中心词向量、上下文词向量),ui代表词wi而vj代表词wj。这时候它的信息熵是:
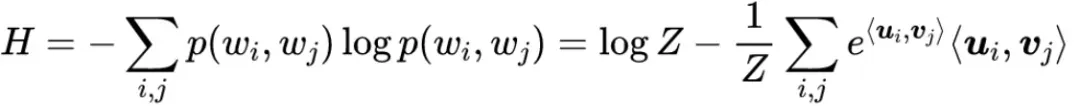
计算上进行近似采样:
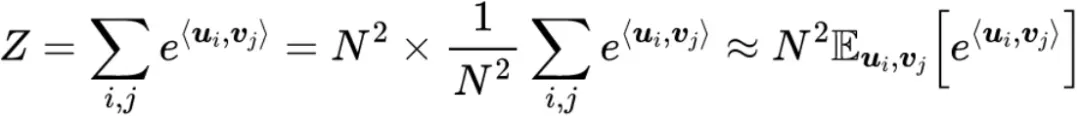
其中,N 是词表大小,同理:
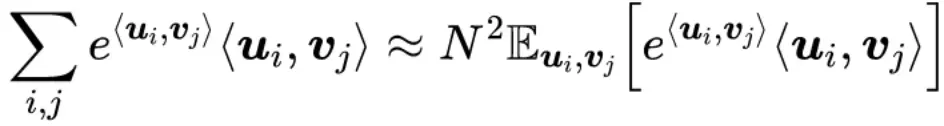
那么,有:
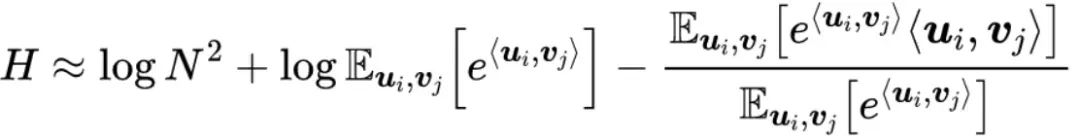
分布假设观察已有的词向量模型,我们可以发现每个维度的数值有正有负,绝对值大小一般也比较均匀。在此,我们不妨假设每个元素的绝对值大概为 1,那么每个词向量的模长大致就为根号n。
并且进一步假设所有的词向量均匀分布在半径为 根号n 的 n 维超球面上,那么 <ui,vj> = ncosθ,θ 是它们的夹,那么:
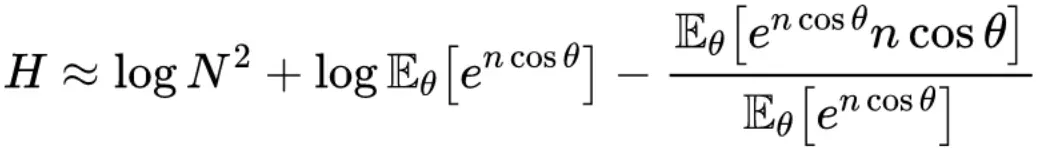
数值计算:
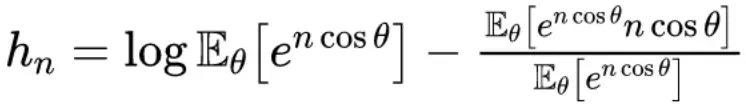
参考:
-
NeurIPS 2018.Word2vec Skip-gram Dimensionality Selection via Sequential Normalized Maximum Likelihood On the Dimensionality of Word Embedding