今天给大家分享机器学习中的一个关键概念,交叉验证。交叉验证(Cross Validation)是一种用于评估机器学习模型性能的技术,主要用于避免过拟合并提高模型的泛化能力。
它通过将数据集划分为多个子集,并在不同的子集上训练和测试模型,以确保模型能够在新的、未见过的数据上表现良好。
交叉验证的原理
交叉验证的核心思想是:将原始数据集划分成若干个子集,然后使用这些子集对模型进行多次训练和测试。这样可以确保每个数据点都被用于训练和测试,从而减少由于数据划分偏差带来的误差。
-
数据划分
将数据集划分成多个互不重叠的子集(或者称为折)。
-
训练与验证
在每次训练中,选择其中一部分数据作为训练集,剩余部分作为验证集(测试集)。
-
评估性能
通过多次迭代训练和测试,计算模型的平均性能,以获得更稳定的评估结果。
常见的交叉验证技术
常见的交叉验证技术包括 K 折交叉验证、留一法交叉验证、分层 K 折交叉验证、时间序列交叉验证等。
一、K 折交叉验证
K 折交叉验证是最常用的一种交叉验证技术,它将数据集随机划分为 K 个大小相等的子集(折)。每个子集依次作为验证集,其余的 K-1 个子集作为训练集来训练模型。这个过程会重复 K 次,确保每个子集都被用作一次验证集。最终的评估结果是这 K 次验证结果的平均值。
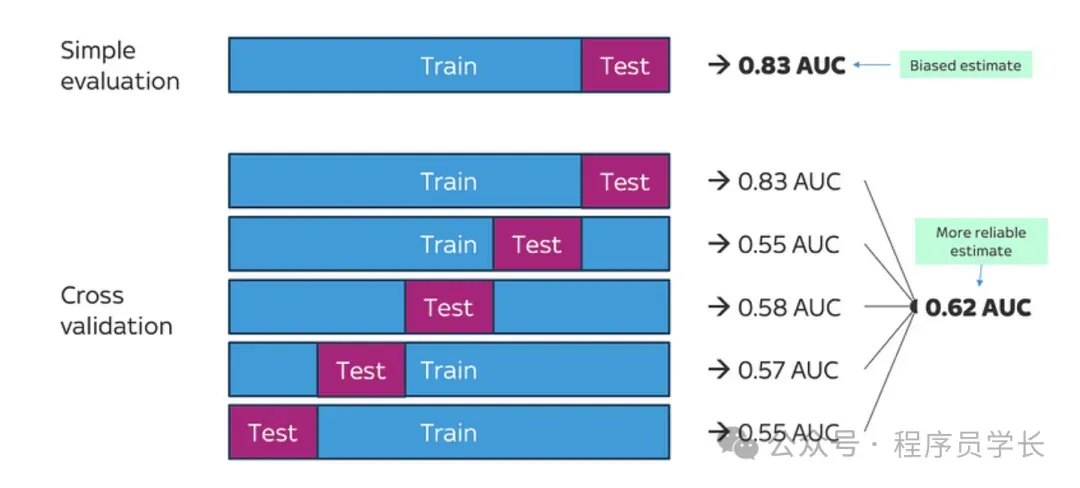
步骤
- 将数据集 D 划分成 K 个子集 D1、D2、D3…DK。
- 对每个 k 从 1 到 K,用 D - Dk(即去除Dk的数据)训练模型,并用 Dk 验证模型。
- 计算每次验证的评估指标(如准确率、均方误差等)。
- 计算所有 K 次验证结果的平均值作为最终评估。
优缺点
优点
- 每个数据点都被用作训练集和验证集,能够较为准确地评估模型性能。
- 适用于样本量有限的情况。
- 可以有效避免过拟合。
缺点
- 计算量较大
from sklearn.model_selection import KFold, cross_val_score
from sklearn.datasets import load_iris
from sklearn.linear_model import LogisticRegression
import numpy as np
# 加载数据集
iris = load_iris()
X, y = iris.data, iris.target
# 定义k折交叉验证
k = 5
kf = KFold(n_splits=k, shuffle=True, random_state=42)
# 定义模型
model = LogisticRegression(max_iter=200)
# 计算交叉验证得分
scores = cross_val_score(model, X, y, cv=kf)
# 输出交叉验证得分
print(f"K-Fold Cross Validation Scores: {scores}")
print(f"Mean Score: {np.mean(scores)}")
二、留一交叉验证 (LOOCV)
留一交叉验证是 K 折交叉验证的特殊形式,其中 K = n,即每次只用一个样本作为验证集,剩余的n-1个样本作为训练集。
这种方法特别适合数据量较小的情形。
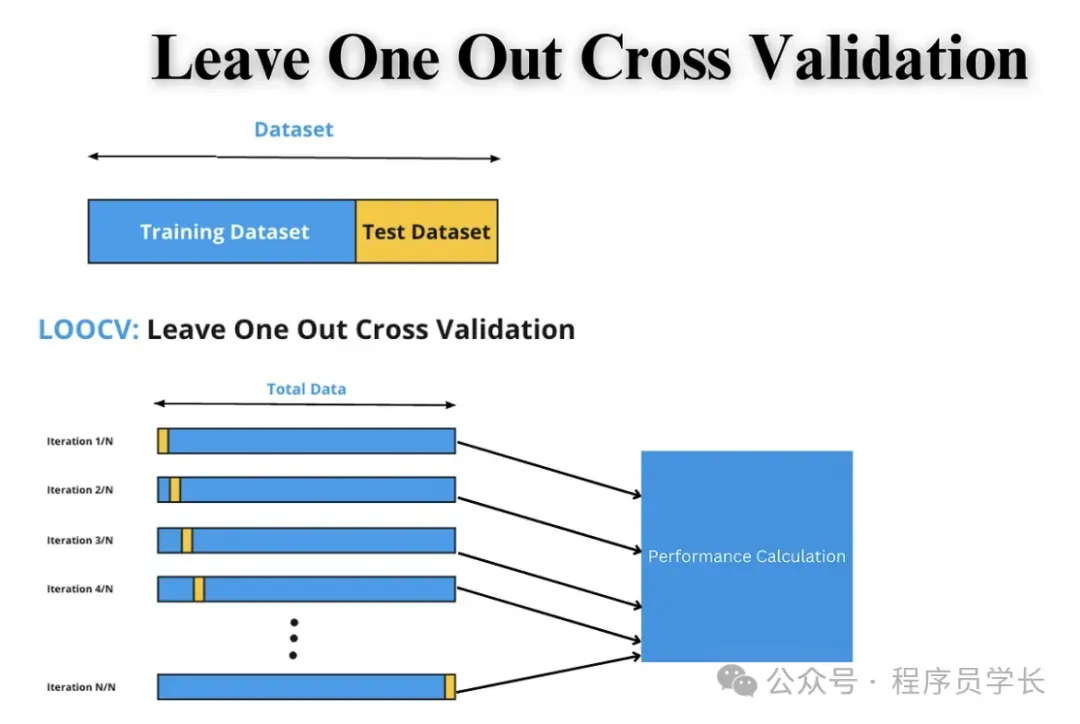
步骤
- 对于每一个数据点 xi,将其作为验证集,其余的n-1个样本作为训练集。
- 在训练集上训练模型,并在验证集 xi 上进行评估。
- 重复这个过程 n 次,确保每个样本都被用作验证集一次。
- 计算所有验证结果的平均值作为最终评估。
优缺点
优点
- 每个数据点都作为验证集,评估结果非常精确。
- 不会浪费数据,适用于小样本数据集。
缺点
- 计算开销非常大,对于大数据集而言,训练和评估的次数非常多,可能导致非常长的计算时间。
from sklearn.model_selection import LeaveOneOut
loo = LeaveOneOut()
scores = cross_val_score(model, X, y, cv=loo)
print(f"LOOCV Mean Score: {np.mean(scores)}")
三、留 P 交叉验证 (LPOCV)
留 P 交叉验证是 LOOCV 的一个扩展,其中在每次迭代中,从数据集中选择 P 个样本作为验证集,剩下的 n - P 个样本作为训练集。
步骤
- 从数据集中随机选择 P 个样本作为验证集。
- 使用其余的 n - P 个样本作为训练集来训练模型。
- 对于每一个验证集,计算评估指标。
- 计算所有 n/p 次验证结果的平均值作为最终评估。
优缺点
优点
- 在数据量较大的情况下,比 LOOCV 计算效率更高。
- 适用于需要进行多次验证,但又不希望每次只选择一个样本作为验证集的情况。
缺点
- 计算复杂度较高
四、分层 K 折交叉验证
分层 K 折交叉验证是一种改进的 K 折交叉验证方法,特别适用于类别不平衡的数据集。
在分类任务中,如果数据集中某些类别的样本数较少,K折交叉验证可能导致验证集中某些类别的样本过少,从而影响评估的准确性。
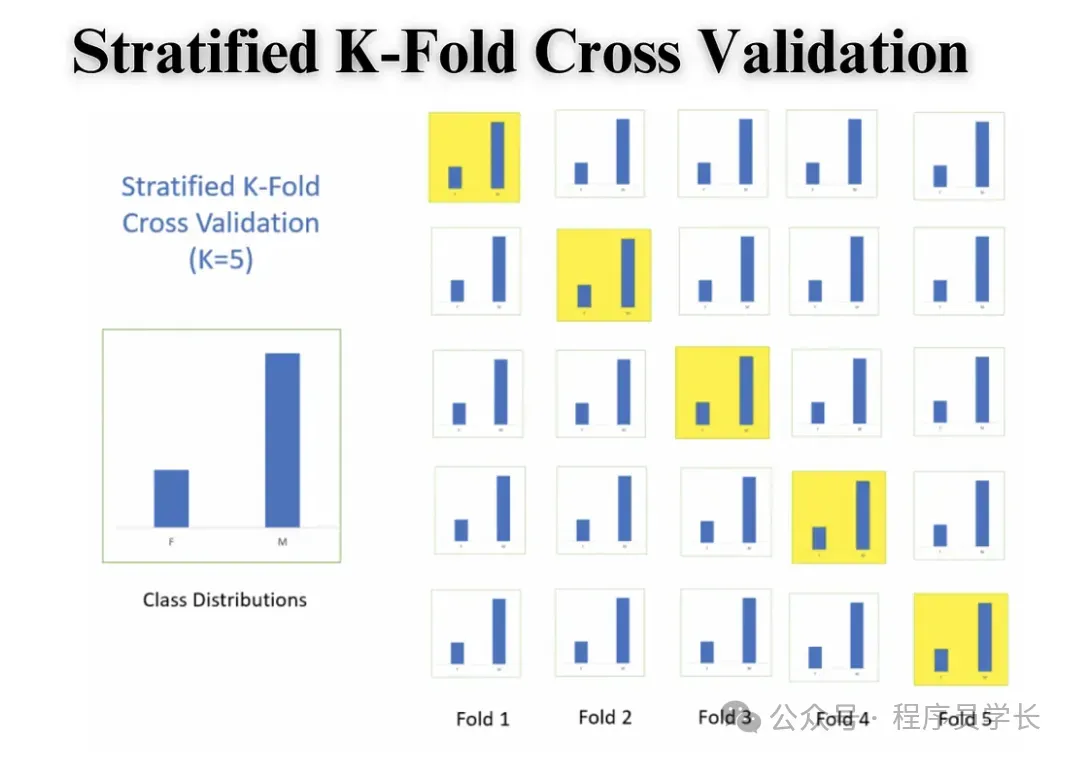
分层K折交叉验证通过确保每个折中各个类别的比例与整个数据集中的比例一致,从而使每个折中的类别分布更加均衡。
步骤:
- 将数据集按照类别标签进行分层,确保每个类别的比例在各个折中保持一致。
- 然后进行与普通 K 折交叉验证相同的过程。
优缺点
优点
- 对于类别不平衡的数据集,能有效避免某些类别在某些折叠中完全消失的情况,从而提高评估的准确性。
- 可以避免在某些类别样本较少的情况下,验证集偏向某一类数据的问题。
缺点
- 由于数据的分层操作,会比普通的 K 折交叉验证更复杂。
from sklearn.model_selection import StratifiedKFold
skf = StratifiedKFold(n_splits=5, shuffle=True, random_state=42)
scores = cross_val_score(model, X, y, cv=skf)
print(f"Stratified K-Fold Mean Score: {np.mean(scores)}")
五、时间序列交叉验证
时间序列交叉验证是一种特殊的交叉验证方法,适用于时间序列数据。
在时间序列数据中,数据点之间具有时间上的依赖关系,因此不能像其他交叉验证方法那样随意打乱数据。
常用的方法包括
-
滚动窗口法(Sliding Window)
在滚动窗口方法中,我们使用一个固定大小的时间窗口进行训练,并在接下来的时间点进行验证。
每次训练集向前滑动一个时间步,保持训练集大小不变。
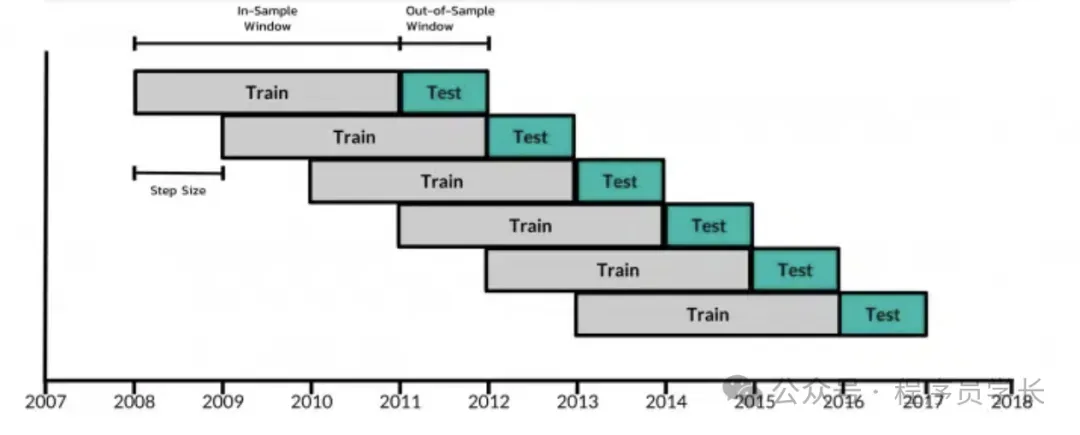
-
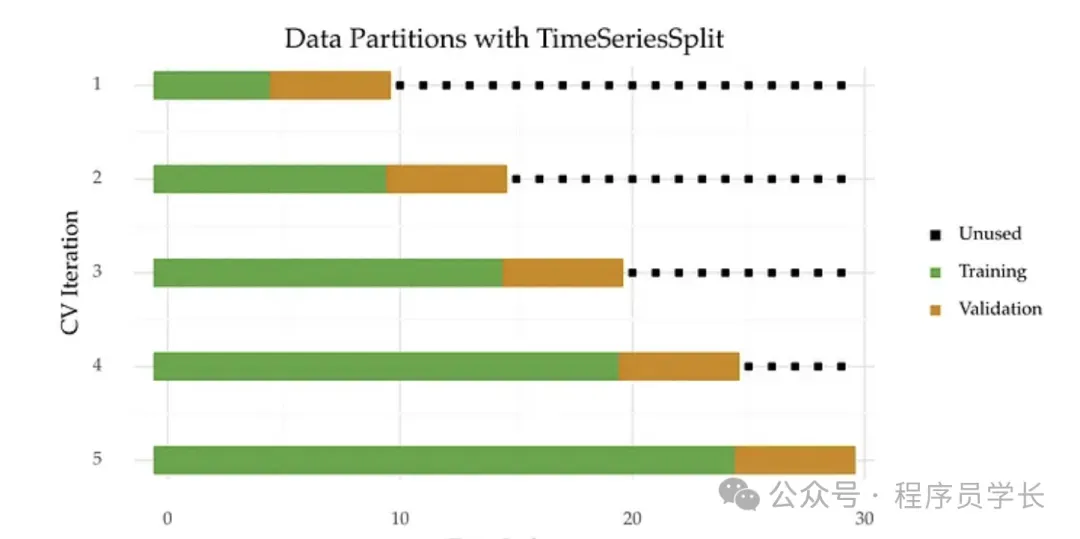
扩展窗口法(Expanding Window)
扩展窗口法与滚动窗口类似,不同之处在于训练集的大小逐步增加,而验证集大小保持不变。
这种方法可以利用所有过去的数据进行训练,使模型更充分地学习时间序列模式。
优缺点
优点
- 适用于时间序列数据,能够有效考虑时间依赖性。
- 模型的训练和测试过程符合时间序列的实际情况,避免了数据泄露。
缺点
- 不能像 K 折交叉验证那样充分利用数据。
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.model_selection import TimeSeriesSplit
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_absolute_error
# 生成示例时间序列数据
np.random.seed(42)
n = 100
time_series_data = pd.DataFrame({
'timestamp': pd.date_range(start='2020-01-01', periods=n, freq='D'),
'feature': np.arange(n) + np.random.normal(0, 5, n), # 递增趋势 + 噪声
'target': np.arange(n) + np.random.normal(0, 3, n) # 目标变量
})
# 定义特征和目标变量
X = time_series_data[['feature']].values
y = time_series_data['target'].values
# 定义时间序列交叉验证
tscv = TimeSeriesSplit(n_splits=5)
# 存储结果
mae_scores = []
# 执行交叉验证
for train_index, test_index in tscv.split(X):
X_train, X_test = X[train_index], X[test_index]
y_train, y_test = y[train_index], y[test_index]
model = LinearRegression()
model.fit(X_train, y_train)
y_pred = model.predict(X_test)
mae = mean_absolute_error(y_test, y_pred)
mae_scores.append(mae)
print(f"Train size: {len(train_index)}, Test size: {len(test_index)}, MAE: {mae:.4f}")
print(f"Mean MAE: {np.mean(mae_scores):.4f}")
文章来源:微信公众号-程序员学长,原始发表时间:2025年03月11日。