在PyTorch框架中,模型的每个训练周期(epoch)都会通过循环迭代的方式,依次执行前向传播与反向传播过程。其中前向传播负责计算预测,反向传播负责通过梯度下降优化参数以最小化损失。
1.前向传播:通过模型(model)计算预测值(predictions)和损失(loss)。
2. 反向传播:利用loss.backward()方法调用PyTorch的autograd模块自动计算梯度,然后通过优化器(optimizer.step())更新模型的参数。
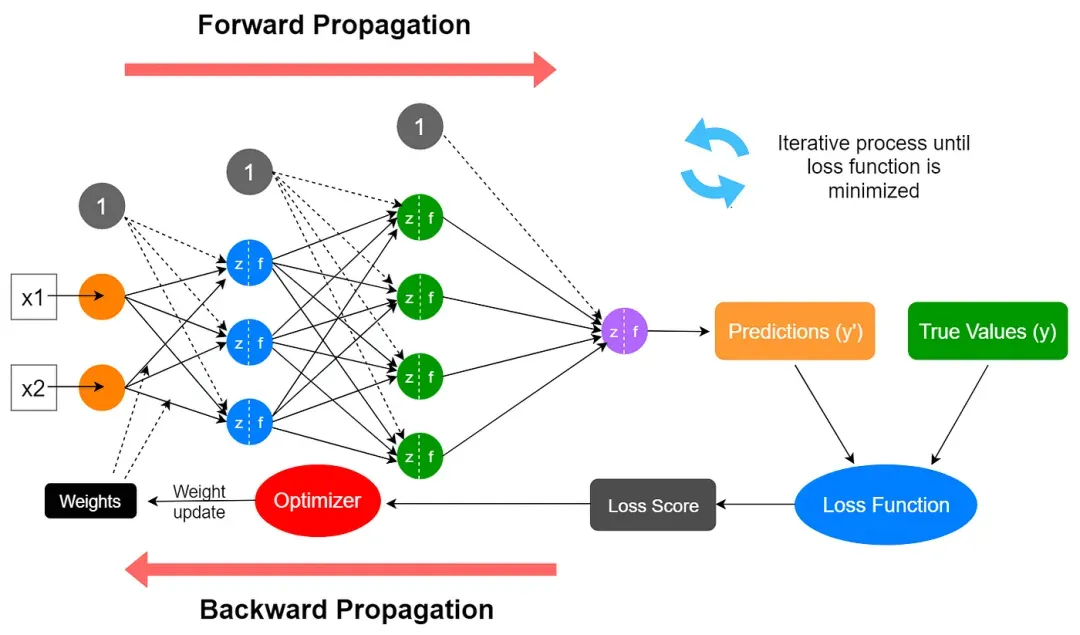
一、前向传播
前向传播(Forward Propagation)是什么?
前向传播是神经网络通过逐层计算,从输入层开始,经过隐藏层,最终到达输出层,以产生预测值的过程。
在这个过程中,输入数据通过网络中的权重和偏置进行线性变换,然后通过激活函数进行非线性变换,得到每一层的输出。最终,输出层的输出即为神经网络的预测值。
一、输入层接收数据
输入层是神经网络的第一层,它接收来自外部的数据。
二、计算隐藏层输出
数据从输入层传递到隐藏层,隐藏层中的每个神经元都会接收来自上一层神经元的输入,并计算其加权和。加权和通过激活函数(如ReLU、Sigmoid、Tanh等)进行非线性变换,生成该神经元的输出。
三、计算输出层输出
输出层是神经网络的最后一层,它接收来自隐藏层的输入,并计算最终的输出。
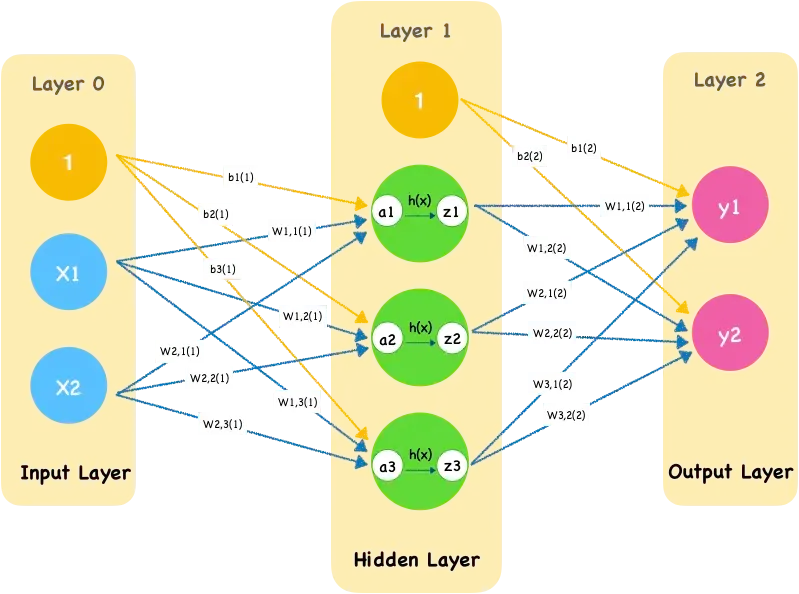
PyTorch如何实现前向传播?在PyTorch中实现前向传播需要基于nn.Module类定义网络结构,并在forward()方法中明确数据流的计算过程。
import torch.nn as nn
class NeuralNetwork(nn.Module):
def __init__(self):
super(NeuralNetwork, self).__init__()
self.flatten = nn.Flatten() # 展平输入(如28x28图像转为784维向量)
self.hidden1 = nn.Linear(784, 128)
self.hidden2 = nn.Linear(128, 64)
self.out = nn.Linear(64, 10) # 输出层(10分类任务)
def forward(self, x):
x = self.flatten(x)
x = self.hidden1(x) # 线性变换
x = torch.relu(x) # 非线性激活
x = self.hidden2(x)
x = torch.sigmoid(x)
x = self.out(x) # 输出层预测值
return x
二、反向传播
反向传播(Backward Propagation)是什么?
反向传播则是根据损失函数计算梯度,并据此更新网络的权重和偏置。
在这个过程中,从输出层开始,使用损失函数逐层计算每个神经元的误差,然后利用这些误差和前一层的激活值来计算当前层权重的梯度(损失函数对权重的偏导数)。最后,使用这些梯度,通过优化算法(如梯度下降)更新网络的参数,以减小损失函数的值。
一、计算误差
在神经网络的训练过程中,我们需要一个衡量模型预测输出与真实输出之间差异的标准,这个标准就是损失函数。常见的损失函数包括均方误差(MSE)、交叉熵损失(Cross-Entropy Loss)等。
二、计算梯度
计算误差后,需要利用链式法则(Chain Rule)将损失函数的值反向传播到网络的每一层,并计算每个权重的梯度。梯度表示了损失函数相对于每个权重的变化率,用于指导调整权重以减小损失函数的值。
三、更新参数
得到每个权重的梯度后,使用梯度下降(Gradient Descent)等优化算法来更新网络的权重和偏置。梯度下降算法的基本思想是沿着梯度的反方向更新权重,以减小损失函数的值。
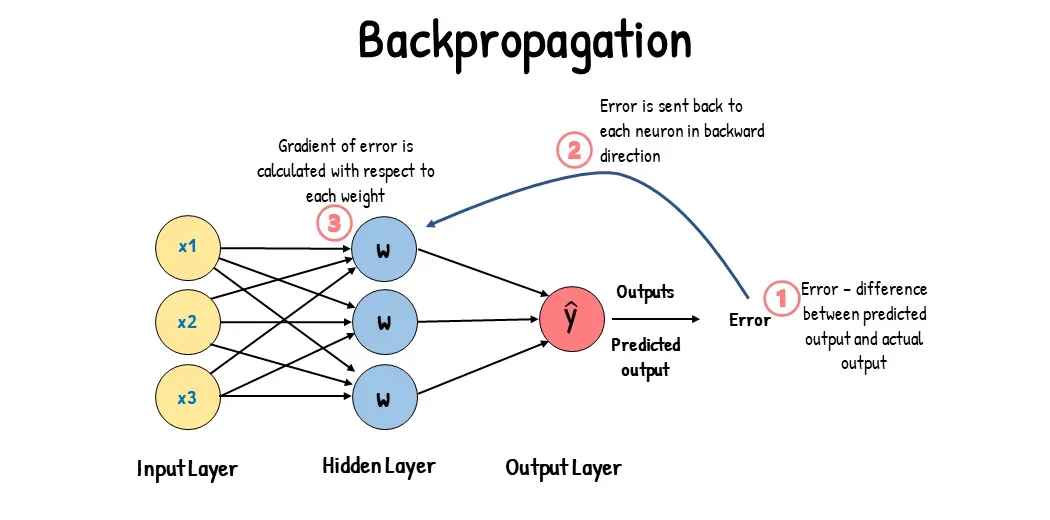
PyTorch如何实现反向传播?在PyTorch中实现反向传播的核心机制是动态计算图和自动微分(Autograd),其过程通过调用loss.backward()触发。
一、动态计算图
在前向传播过程中,PyTorch会自动追踪所有涉及可训练参数的操作,构建动态计算图。
二、自动微分(Autograd)
PyTorch的autograd模块通过链式法则逐层计算损失函数对参数的梯度。梯度计算从输出层(损失值)开始,反向传播至输入层。
# 前向传播与损失计算
optimizer = torch.optim.SGD(model.parameters(), lr=0.01)
loss_fn = torch.nn.MSELoss()
for epoch in range(100):
y_pred = model(x) # 前向传播
loss = loss_fn(y_pred, y) # 计算损失
optimizer.zero_grad() # 清空梯度
loss.backward() # 反向传播计算梯度
optimizer.step() # 参数更新
文章来源:微信公众号-架构师带你玩转AI,原始发表时间:2025年03月11日。